材料力学笔记

材料力学是一门非常重要的课程，它的知识点可以说是贯穿了整个大学后半段。

基于《材料力学Ⅰ》（ISBN：978-7-04-030895-2）、《材料力学Ⅱ》（ISBN：978-7-04-030894-5）

平面图形的几何性质

基本概念

1.静矩：Sz = ∫ydA(A)，Sy = ∫zdA(A)。其中：y为到z轴距离，z为到y轴距离

2.组合图形静矩：Sz = ∑(yi·Ai)(i=1,n)，各个部分对同一轴静矩的代数和

3.形心：y = ∫ydA(A) / A = Sz / A（由此可以看出：静矩为0，轴过形心）

4.组合图形形心：y = ∑(yi·Ai)(i=1,n) / ∑Ai(i=1,n)

5.惯性矩：Iz = ∫y²dA(A)。其中：y为到z轴距离。

1. ①矩形惯性矩：Iz = hb³/12 。其中：h为∥边的高度，b为⊥边的高度，坐标原点为形心
   Iz = ∫y²dA(A) = ∫(-b/2,b/2)dy∫z²(-h/2,h/2)dz = 1/3·(h/2)³·2·b = hb³/12
2. ②圆惯性矩：Iz = πD^4/64，坐标原点为形心
   Iz = ∫dθ(0,2π)∫ρ²cos²θ·ρ(0,D/2)dρ = 1/4·(D/2)³·π/2 = πD²/64
3. ③圆环：Iz = π(D^4-d^4)/64，坐标原点为形心
4. ④组合图形惯性矩：Iz = ∑Iz(i=1,n)，对同一根轴

6.极惯性矩：Iρ = ∫ρ²dA(A) = Iy² + Iz²。其中，ρ为到原点距离。Iρ = ∫ρ²dA(A) = ∫(y²+z²)dA(A) = Iy² + Iz²

7.惯性半径：Iz = iz²·A。即iz = sqrt(Iz/A)。圆截面惯性半径为D/4

8.惯性积：Iyz = ∫yzdA(A)。注：任意坐标轴为对称轴则Iyz=0

轴的变换

1.平行移轴公式：Izo = Izc + y(oc)²·A；Ixyo = Ixyc + x(oc)y(oc)·A。其中，O为新坐标轴，C为形心坐标轴。∫y²dA(A) = ∫[y+y(oc)]²dA(A) = ∫y²dA(A) + ∫y(oc)²dA(A) + 2y(oc)·∫ydA(A)(值为0)
（通过这个式子，可以很方便的计算组合图形的惯性轴）

2.转轴公式：

1. Iy1 = Iycos²α + Izsin²α - 2Iyzcosαsinα = (Iy+Iz)/2 + (Iy-Iz)/2·cos2α - Iyz·sin2α。其中：α为新轴y1,x1相对旧轴y,x转动的角度。（个人认为前面一个式子比较好记，所以加粗了）
   新轴和旧轴之间的关系：y1=ycosα+zsinα；z1=zcosα-ysinα(由后图几何关系可知) -> Iz1 = ∫y1²dA(A) = ∫(ycosα+zsinα)²dA(A) = Iycos²α + Izsin²α - 2Iyzcosαsinα
2. Iz1 = Izcos²α + Iysin²α + 2Iyzcosαsinα = (Iz+Iy)/2 + (Iz-Iy)/2·cos2α + Iyz·sin2α
3. Ixy1 = (Iy-Iz)/2·sin2α + Iyz·cos2α

形心主惯性轴

1.用途：用于应力应变分析的计算

2.要素：①过形心②Iyz=0（满足这一点的称为主轴）

3.特点：两个主惯性距Iy，Iz分别为I的最大值和最小值

4.求解：

1. 形心主惯性轴与形心轴的夹角α0：tan2α0=-2Iyz/(Iy-Iz)令转轴公式的Ixy1=0，化简可得
2. 形心主惯性矩Iy0 = (Iy-Iz)/2 + sqrt{[(Iy-Iz)/2]²+Iyz²}；Iz0 = (Iy-Iz)/2 - sqrt{[(Iy-Iz)/2]²+Iyz²}将α带入各表达式，化简可得

杆件变形的基本形式

基本概念

总结及注意事项

名称	正应力	变形	切应力	转角	说明
拉压	σ=F/A	∆l=Fl/EA	-	-	-
扭转	-	-	τ=T/Wt(圆轴) =Me/(2Aδ)(圆筒)	ψ’=T/(GIp)	δ为厚度ψ’为转角的倒数
弯曲	σ=My/Iz =M/W(最大)	w’’=M/EI	τ=FsSz/Izb	θ=w’	w为挠度，θ为转角，z为对中性轴，b为到中性轴距离

1.应变不是长度，而是变化的长度/原始长度

2.三个弹性常数之间的关系：G=E/[2(1+μ)]

3.抗扭截面系数Wt=Ip/R；抗弯截面系数W=Iz/y(max)

4.圆轴扭转应力公式推导：①由于几何关系，距圆心为ρ处的切应变γ=ρ·dφ/dx（dφ为轴中长为dx的微端因扭转而转过的角度）aa'=ρdφ=γdx（aa'为选取的一弧长）②由物理关系τ=Gγ得τ=Gρ·dφ/dx③由静力关系扭矩T=∫ρτdA(A)=G·dφ/dx∫ρ²dA(A)=G·dφ/dx·Ip（Ip为极惯性矩），将τ=Gρ·dφ/dx带入上式得任一点切应力τ=Tρ/Ip（T为扭矩），因此最大切应力τ(max)=TR/Ip=T/Wt（Wt为抗扭截面系数，Wt=Ip/R）

5.计算弯曲变形有很多种方法，比如说积分法，叠加法，能量法等等

能量相关

1.杆件变形能的计算

类型	应变能
拉压	Vε = ∫ F²(x)/2EA · dx(→l)
纯剪切	Vε = ∬ 1/2·τγ dA(→A)
扭转	Vε = ∫ T²(x)/2GIp · dx(→l)
弯曲	Vε = ∫ M²(x)/2EI · dx(→l)

2.当位移与外力呈线性关系时，有 Vε = ∫ F²(x)/2EA · dx + ∫ T²(x)/2GIp · dx + ∫ M²(x)/2EI · dx

3.功的互等定理：第一组力在第二组引起的位移上所作的功，等于第二组力在第一组引起的位移上所作个功Δ

4.莫尔积分：Δ = ∑ F(x)F‘(x)/EA · dx + ∫ T(x)T’(x)/GIp · dx + ∫ M(x)M‘(x)/EI · dx （F‘(x)、T’(x)、M‘(x)为在所求单位力作用下的力、扭矩、弯矩方程）

5.莫尔积分图乘法：Δ = ∫ ωM‘(C) / EI（其中ω为M(x)图面积，M‘(C)为M(x)图形心对应M’(x)的值）

超静定相关

超静定问题主要分为两大类：外力超静定和内力超静定。

1.对于外力超静定：

①判定静不定次数

②选取并去除多余约束，以多余约束反力。选取基本静定基，在基本静定基加原载荷,并加多余约束反力X1，得到相当系统。

③画出两个图：原载荷图和单位力图。(或写出内力方程)

1. 在基本静定基上加原载荷，画原载荷图 (或写出内力方程)
2. 在基本静定基上沿所求未知力方向加广义单位力，画单位力图 (或写出内力方程)

④计算正则方程的系数： Δ1p和δ11，两图互乘得Δ1p，单位力图自乘得δ11。或用莫尔积分求系数。

⑤建立力法正则方程和求解：Δ1p + δ11·X1 = 0

2.对内力超静定问题，是将上述第二点换为：将一段杆打断，用力X1代替，得到相当系统

应力应变分析

基本概念

1.应力应变分析研究的是一点处的应力状态，用单元体表示。一点有六个独立的应力分量

2.主平面：剪应力为零的截面。主应力：主平面上的正应力。

3.实例：

变形类型	应力状态
拉压	←□→
扭转	↓□↑（上方→；下方←）
弯曲	→↓□↑←（上方→；下方←）（内部任意一点）

二向应力状态分析

1.任意斜截面上的上的应力：

1. ①σα = (σx + σy)/2 + (σx - σy)/2·cos2α - τxy·sin2α

2. ②τα = (σx - σy)/2·sin2α + τxy·cos2α

   其中：α为斜截面外法线与x轴的夹角，逆时针为正；正应力拉为正压为负；切应力顺时针为正。τxy中的x表示作用平面的法线方向，y为平行的方向

2.最大正应力和最小正应力

σmax/σmin = (σx + σy)/2 ± sqrt{ [(σx - σy)/2]² + τxy² }

3.主应力与主平面

令上式 τα= 0 可以得到主平面的方位，即 tan2α0 = - 2τxy/(σx - σy)

4.应力圆画法

1. 建立应力坐标系 τ-σ （注意选好比例尺）
2. 在坐标系内画出点A(σx，τxy)和B(σy，τyx)
3. AB与σ轴的交点C为圆心，AC=BC为半径的圆为应力圆

三向应力状态分析

1.一点的最大正应力 σmax = σ1

2.一点的最大切应力 τmax= (σ1 - σ3)/2

平面应变状态分析

1.应力与应变的转化：广义胡克定理

1. ①εx = 1/E · [σx - μ( σy + σz ) ]；εy = 1/E · [σy - μ( σx + σz ) ]；εz = 1/E · [σz - μ( σy + σx ) ]
2. ②γxy = τxy / G；γyz = τyz / G；γzx = τzx / G；

因此可以得到主应力与主应变的关系：

1. ①ε1 = 1/E · [σ1 - μ( σ2 + σ3 ) ]
2. ②ε2 = 1/E · [σ2 - μ( σ3 + σ1 ) ]
3. ③ε3 = 1/E · [σ3 - μ( σ1+ σ2 ) ]
4. ④γxy = γyz = γzx = 0

2.主应力与主应变的计算公式完全相似，只是将式中的正应力改为正应变；切应力改为切应变/2即可

3.体应变 θ = ε1 + ε2 +ε3

补充

切应力互等原理：在平衡的单元体内，如果存在切应力，则有切应力成对存在且数值相等；两者垂直于两个平面的交线，方向共同指向或背离这个交线。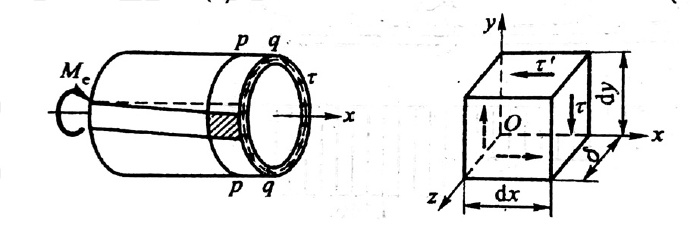

（τ’产生的原因：为了保持单元体的平衡）

强度理论

强度理论是关于“构件发生强度失效起因”的假说，它是否正确，适用于什么情况，必须由生产实践来检验。强度理论分成两类：一类解释断裂失效：另一类解释屈服失效。

1.始种常见的强度理论

强度理论	相当应力	说明	适用范围
第一强度理论	σr1 = σ1	最大拉应力是引起材料脆断破坏的因素。	脆性材料二轴拉伸；三向受拉
第二强度理论	σr2 = σ1 - μ( σ2 + σ3 )	最大伸长线应变是引起材料脆断破坏的因素。	-
第三强度理论	σr3 = σ1 - σ3	最大切应力是引起材料屈服的因素。	塑性材料；三向受压
第四强度理论	σr4 = sqrt{ 1/2·[ ( σ1 - σ2 )² + ( σ2 - σ3 )² + ( σ3 - σ1 )² ] }	形状改变比能是引起材料屈服的因素。	塑性材料；三向受压
莫尔强度理论	σrM = σ1 - [σt]/[σc] · σ3	考虑了材料抗拉和抗压强度不相等的情况的第三强度理论。	材料抗拉和抗压强度不等；脆性材料一拉一压

2.对于典型二向应力状态：σr3 = sqrt( σ² + 4τ² )；σr4 = sqrt( σ² + 3τ² )

组合变形相关

1.研究方法：

①外力分析：外力向形心简化并沿主惯性轴分解；

②内力分析：求每个外力分量对应的内力方程和内力图，确定危险面；

③应力分析：画危险面应力分布图，叠加，建立危险点的强度条件。

2.对于弯扭组合

1. 按照第三强度理论，有σr3 = 1/W · sqrt( M² + T² )
2. 按照第四强度理论，有σr4 = 1/W · sqrt( M² + 0.75T² )

压杆稳定

1.概念：工程中有些构件具有足够的强度、刚度，却不一定能安全可靠地工作，这是因为稳定性不够。细长杆件受压时轴线先开始是直线，接着必然是压弯。因此这里有一个极限值Fcr(临界压力)：由稳定平衡转化为不稳定平衡时所受轴向压力的界限值，称为临界压力。

2.临界压力：Fcr = π²EI / (μl)²

其中：μ 为长度系数，μl为相当长度

两端铰支	一段固定一端自由	一端固定一段铰支	两端固定
μ = 1	μ = 2	μ = 0.7	μ = 0.5

3.临界应力：

其中：λ称为柔度；极惯性矩 i = sqrt(I / A)）

欧拉公式σcr = π²E / λ² 推导：σcr = Fcr / A = π²EI / A·(μl)² = π²E · (μl / i)²

注：欧拉公式适用于大柔力杆（λ ≥ λ1 = π·sqrt( E/σp )）

4.安全因数 nst = Fcr / F