机械原理笔记

一半是几何画图，一半是理论力学的应用，哦，还有个齿轮的计算。画图相关的现在都用计算机辅助软件了，估计过几年这门课就要改版了。

参考资料：《机械原理与机械设计》第三版（ISBN：978-7-04-039981-3）

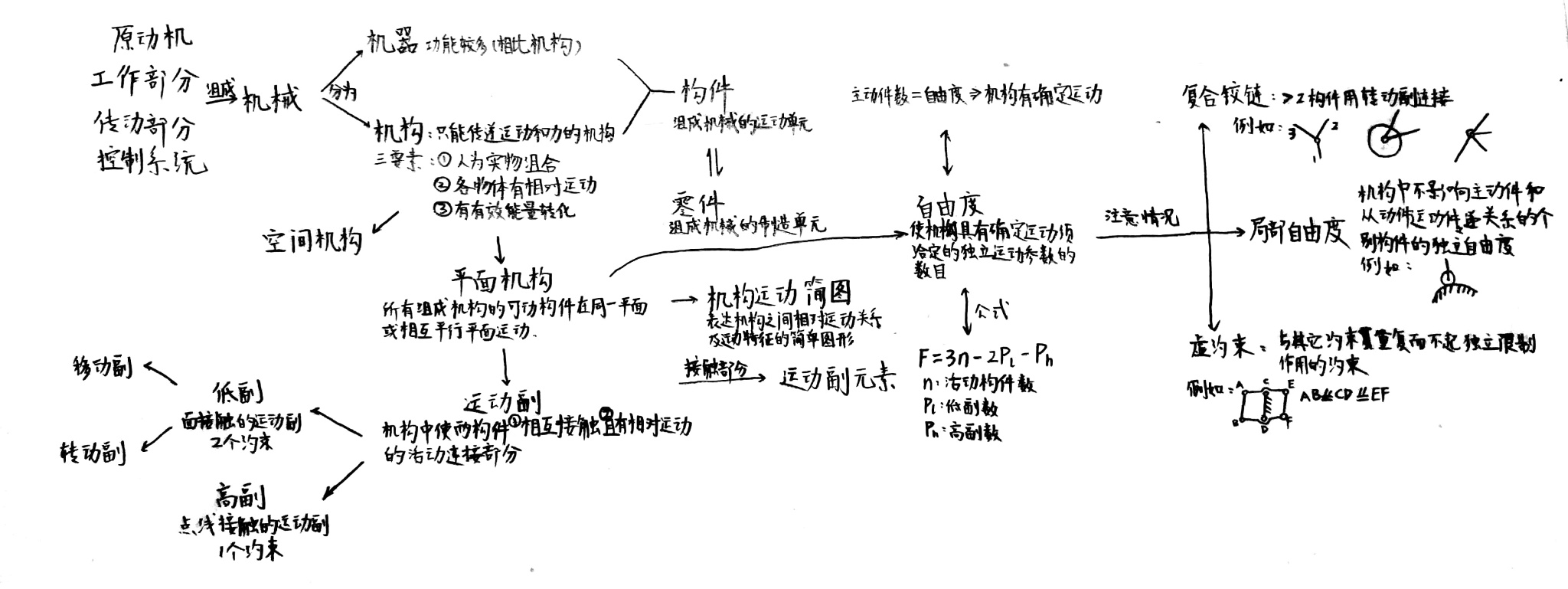
平面连杆机构

平面连杆机构的基本特性

平面四杆机构的基本形式是铰链四杆机构。运动副均为转动副的四连杆机构称为铰链四连杆机构。铰链四连杆机构中，能够整周回转的连架杆称为曲柄，不能的连架杆称为摇杆。按照连架杆的不同，又分为曲柄摇杆机构、双曲柄机构、双摇杆机构

曲柄存在的条件

当连架杆可以共线时，就可以存在曲柄

根据几何关系可以得到曲杆存在的条件：①最短杆与最长杆长度之和≤其他两杆长度之和②最短杆做连架杆或机架

总结可以得到，在满足上式①条件后：

做机架的杆	机构类型
最短杆	双曲柄机构
最短杆临边	曲柄连杆机构
最短杆对边	双连杆机构

急回运动特性

曲柄运动的时候做等速运动，而从动件在往返这两个阶段速度是不一样的，这就是急回运动特性，急回程度可以用行程变化系数K表示，K = 输出构件回程的平均速度/输出构件工作行程的平均速度

在曲柄摇杆机构中，曲柄与连杆两次共线的夹角称为极位夹角θ（θ为锐角），摇杆在这两个位置的夹角称为摆角

极位夹角θ与K的关系：θ = 180° · (K-1)/(K+1)，其中当θ = 0时，K=1，机构无急回特性

压力角与传动角

压力角：主动件通过连杆作用于从动件的力 与 从动件作用点绝对速度 的方向所夹的锐角

死点位置

主动件做往复运动时，存在死点位置（从动件无法从主动件获得力的位置）。

凸轮机构

1.优点：只要设计出适当的轮廓，即可实现特定的运动规律。结构简单，工作可靠

2.缺点：高副接触，压强较大，容易磨损，且费用较高。

凸轮基本概念介绍

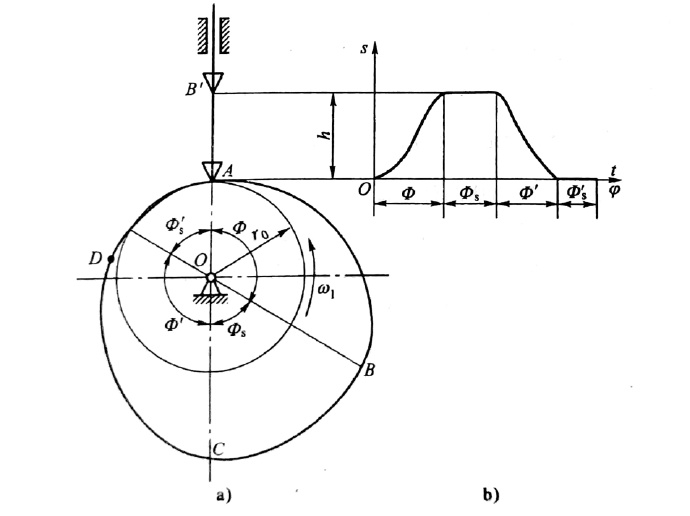
1.基圆：以凸轮轮廓最小向径r0为半径所作的圆，r0为基圆半径

2.推程：从动件逐渐远离轴心的过程，此时转过的角度为推程运动角

3.回城：从动件由最高位置回到最低位置的过程，此时转过的角度为回程运动角

4.远休止角：推程结束到回程开始出所转动的夹角；近休止角：回程结束到推程开始出所转动的夹角

从动件常见运动规律

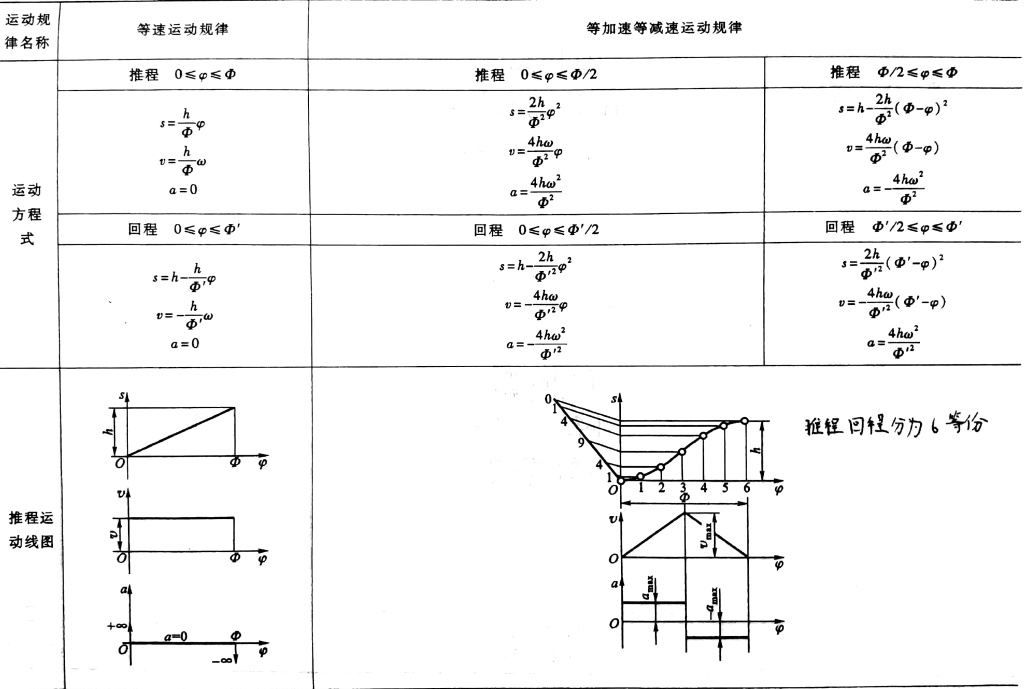
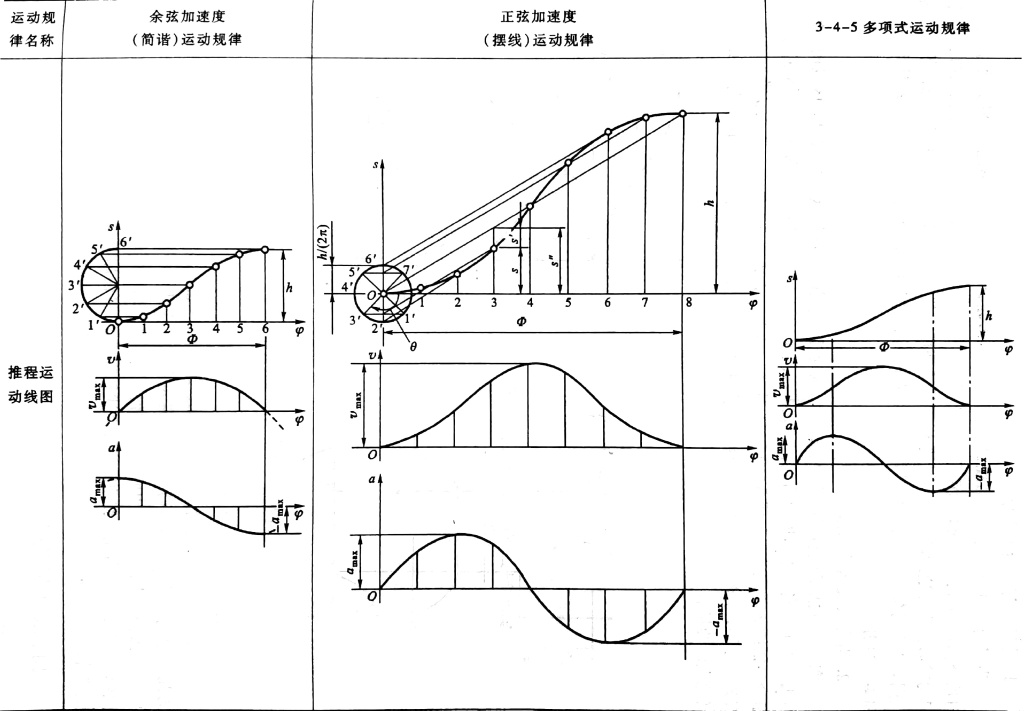
注：在等速运动规律中，运动的起点处和终点处速度发生了突变，机构会受到刚性冲击，等加速减速运动规律和余弦运动规律加速度产生突变，机构会受到柔性冲击

凸轮设计时的注意事项

1.压力角随基圆半径的增大而减小

2.为了防止凸轮运动的失真，可以在滚子半径保持不变的状态下，将基圆半径变小

齿轮机构

闲暇时做的视频

齿轮基本概念介绍

齿廓

我们的齿轮要求传动平稳。传动平稳，就是指在齿轮啮合中，传动比 i=ω1/ω2 为一常数。

由公式推导可得：要使传动比为常数，就需要齿轮轮廓能实现：无论在齿廓的哪一点接触（K点，未标出），过接触点（K）所作的两齿廓的公法线（n）必须与连心线（O1O2）交于一点（C）。这就是齿轮啮合基本定律，满足这个条件的齿廓叫共轭齿廓

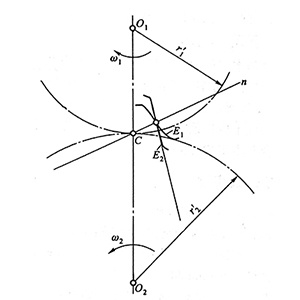
这里提出一个概念：节圆。节圆是以O1、O2为圆心，以轮廓公法线与连心线交点（C）为半径的圆。

在机械中，常常使用渐开线，摆线或圆弧等等曲线作为轮廓线。而渐开线的运用最为广泛。

渐开线

渐开线是由直线沿圆作纯滚动时，直线上任意一点的轨迹。（我们把直线称为发生线，圆称为基圆，轨迹对应中心角叫展角。）

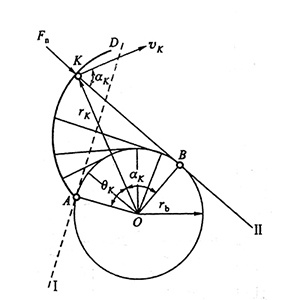
其中：
1.直线长BK=弧长AB

2.渐开线任意法线与基圆相切（由此可推出渐开线符合齿轮啮合基本定律）

3.基圆越小，渐开线越弯曲

4.同一基圆任意两渐开线法向距离相等

5.压力角α=Rb（基圆半径）/OK，即基圆半径与向径的比值

6.基圆内无渐开线

7.渐开线方程：θ=tanα-α（这个式子也是求展角/压力角的式子）

渐开线齿轮

1.传动比=基圆半径的反比，即i12=r2/r1

2.可分性：在安装中即使有偏差，可可以保持传动比为定值（齿轮基圆半径不变，传动比不变）

3.啮合线：渐开线齿廓接触点轨迹

4.啮合角：啮合线与节圆公切线的夹角，用α’表示。

齿轮基本参数

名称	代号	计算公式	备注
模数	m	根据强度计算或结构需要而定	m为标准值
齿数	z	根据强度计算或结构需要而定
中心距	a	a=m(z1+z2)/2
压力角	α	α=20°	α为标准值
分度圆直径	d	d1=mz1,d2=mz2
齿距	p	p=πm	分度圆上
齿厚	s	p=πm/2	分度圆上
齿槽宽	e	p=πm/2	分度圆上
基圆直径	db	db=dcosα=mzcosα
基圆齿距	pb	pb=πmcosα=mzcosα
齿顶圆直径	da	da=m(z+2)
齿根圆直径	df	df=m(z-2.5)
齿顶高	ha	ha=ha❀×m=m	ha❀为标准值=1
齿根高	hf	hf=（ha❀+c❀）m=1.25m	c❀为标准值=0.25

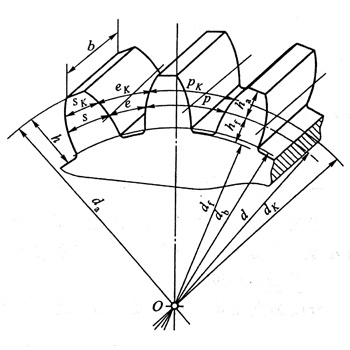
齿条

没什么需要注意的……

内齿轮

齿顶圆直径：da=d+2ha；齿顶圆直径：df=d-2hf（就是正负号换了一下而已）

对于内齿轮，齿顶圆必须大于基圆，为了使内齿轮齿廓全为渐开线

渐开线标准直齿轮

齿轮传动的正确啮合条件

模数和压力角同时相等，即m1=m2,α1=α2
（正确啮合即齿距p相同 => p1=πm2cosα1=p2=πm2cosα2 => m1cosα1=m2cosα2）

齿轮传动的连续性条件

1.端面作用弧：从啮合开始到啮合结束，所转动的分度圆弧长（CD）

2.端面作用角φα=弧长CD/分度圆半径r：端面作用弧所对应的圆心角

3.齿距角τ=齿距p/分度圆半径r：齿距p所对圆心角

重合度

1.定义式：εα=φα/τ，是实际啮合线与齿距的比值。

2.计算式：εα=[z1(tanαa1-tanα’)+z2(tanαa2-tanα’)]/2π。

其中αa1、αa2为1、2齿轮压力角，其值为αa1=acos(rb1/ra1)、αa2=acos(rb2/ra2)、α’=acos(rb/r’)

3.意义 ：εα越大，表示同时啮合的轮齿数越多。齿轮传动越平稳，承载能力越高

例如：εα=1.45表示平均1.45对齿轮参与啮合

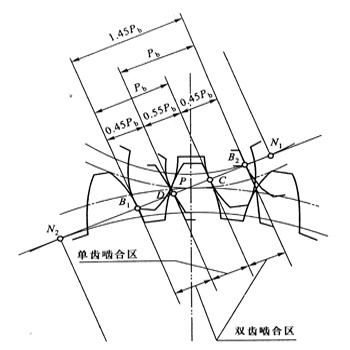
无侧隙啮合条件

a’cosα’=acosα

其中：a为标准中心距，a’为实际中心距，α为压力角，α’为啮合角

• 注：对于齿条而言，无论是否标准安装，啮合角等于分度圆压力角，齿轮节圆与分度圆恒重合

渐开线齿轮切齿原理

加工方法

1.仿形法：刀具的形状为齿槽齿廓的形状，然后直着切下去，形成渐开线齿廓
缺点：齿轮精度低，生产率低，所需刀具多；优点：设备简单

2.范成法：利用一对齿轮啮合时其共轭齿廓互为包络线的原理，将刀具做成齿轮形状，让它一边上下运动进行切割，一边与齿坯啮合。该啮合运动称为展成运动。
优点：加工精确，统一刀具加工的不同齿距的刀也可以正确啮合

根切

1.概念：范成法加工时，如果齿轮齿数过少，可能齿根的渐开线轮廓会被切去一部分

2.原因：刀具的齿顶线与啮合线的交点超过了理论啮合线的极限点N1。
（在保证齿坯分度圆与机床节线相切的前提下，如果齿数过小，会导致基圆半径过小；又因为模数一定，齿高也就确定了；这样的话会使刀具相对基圆切的更深，从而超过理论啮合线的极限点N1。在这种情况下，刀具过理论啮合线的极限点后，依然会切割，这样就产生了根切现象）

3.最少齿数z(min)=2·ha❀/sin²α=17（推导过程：刀具高(ha❀·m)必须在理论啮合点下方 => ha❀·m<mz·sinα·sinα => z(min)=2·ha❀/sin²α）
即标准直齿轮不发生根切的最少齿数为17

变位齿轮

为了避免出现根切现象，我们改变刀具的位置，让刀具远离一段距离，从而解决这个问题。使用这种方法制造出的齿轮为变位齿轮。以标准齿轮的位置为基准，刀具沿径向改变的位置为xm，其中x为变位系数。规定刀具远离轮坯中心为正，靠近为负。

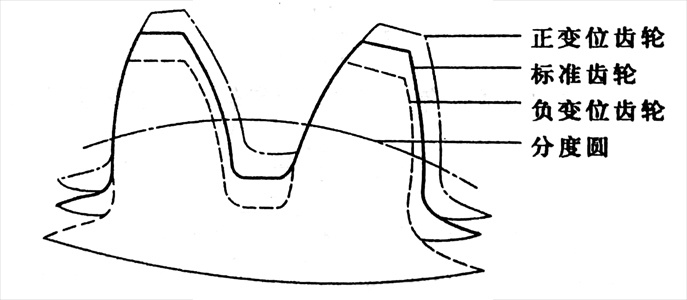
如图，以正变位为例，刀具变位后：
p=(加工刀具齿距为定值)，Ra++(齿顶圆半径)，Rb=(基圆)，R=(分度圆)，Rf++(齿底圆半径)，ha++(齿顶高)，h=(加工刀具齿高为定值)，hf++(齿底高)，e—(齿槽宽)，s++(齿厚宽)，Ra++(齿顶圆半径)，Rf++(齿底圆半径)

最小变位系数

变位需要有一个数值，我们把避免根切的最小的变位系数称为最小变变位系数

• 经过推导得z(min)=(17-z)/17

上式说明：当z<17时，为避免根切，刀具正变位量最小为x(min)m；当z>17时，必要时可以使用负变位（一般是在凑中心距时应用）

无侧隙啮合方程

变位之后，齿轮啮合中心距就发生了改变，而为了保证齿轮之间继续啮合，需要：一轮节圆的齿槽宽等于另一轮节圆的齿厚宽。

经过一系列推导得：tanα’-α’=2(x1+x2)/(z1+z2)·tanα+tanα-α

这个式子常与a’cosα’=acosα结合起来求解

变位齿轮传动类型

• 前排提示：小齿轮相比大齿轮更容易损耗，因此一般x1>x2（1为小齿轮）
  1.零传动 x1+x2=0

1.1标准齿轮传动 x1=x2=0

1.2等变位齿轮 x1=-x2!=0

• 注意：①齿数之和>=34 ②实际中心距小于标准中心距

2.正传动 x1+x2>0

• 注意：实际中心距大于标准中心距

• 当x2=0时，虽然变位系数为0，但大齿轮依然是变位齿轮。
  （这是因为需要无侧隙安装，即需要一轮齿顶圆齿厚=另一轮齿根圆齿槽宽，解决这个的方法是将两轮的齿顶切去一些）

• 优点：减轻齿轮磨损；减少结构尺寸；提高强度

• 缺点：降低了重合度（啮合角增大）

3.负传动 x1+x2>0

• 注意：实际中心距小于标准中心距

• 同理，当x1=0时，虽然变位系数为0，但小齿轮依然是变位齿轮。

• 负传动会加快齿轮损耗，不得以才为之

斜齿圆柱齿轮

• 优点：①传动稳定②重合度大③避免根切的最小尺寸小
• 缺点：有轴向力

齿廓

渐开线螺旋面：与圆柱母线成βb角的斜直线KK’，与圆相切形成的发生面，在做纯滚动时形成的轮廓。其中斜直线KK’与母线的夹角为基圆螺旋角βb。

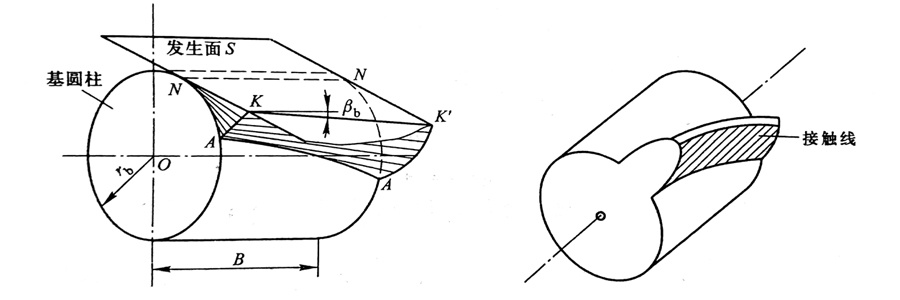
由于是斜齿轮，当一个齿开始啮合时，齿的后部尚未啮合，此时，啮合线为一个点。随着啮合的进行，啮合线会逐渐增大，到某一位置后又会逐渐减少。，然后脱离啮合

基本参数

斜齿轮有两种参数：端面参数（垂直于轴线）、法面参数（垂直于分度圆上螺旋线）。

其中注意：法面齿廓不是渐开线，且法面”圆”为椭圆

根据斜齿轮的展开图（其中：b为齿宽）

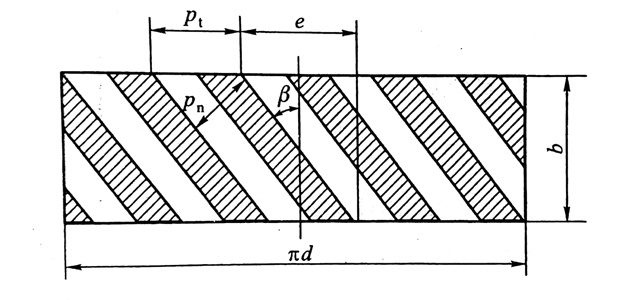
端面参数与法面参数有以下关系

名称	关系	备注
齿距	pt=pn/cosβ	分度圆上
模数	mt=mn/cosβ	分度圆上
压力角	tan(αt)=tan(αn)/cosβ	分度圆上

注：根据制造方式，法面尺寸为标准值

齿轮正确啮合条件

模数和压力角分别相等，外啮合时螺旋角相反，内啮合时螺旋角相同。
即：

1.mt1=mt2(mn1=mn2);

2.αt1=αt2(αt1=αt2);

3.β1=-β2(外啮合)/β1=β2(内啮合)

• 注：左旋：沿齿轮的轴向观察，〼为右旋，反之为左旋

重合度

εγ=α（端面重合度）+εβ（纵向重合度）=εα + bsinβ/pn= [z1(tanαa1-tanα’)+z2(tanαa2-tanα’)]/2π + bsinβ/pn

当量齿数

由于斜齿圆柱齿轮法向齿形不是渐开线就引入了当量齿轮的概念。当量齿轮是 刀具沿法向加工时 为了模拟出相似的齿形 而假想的直齿圆柱齿轮。
具体模拟方法如下：

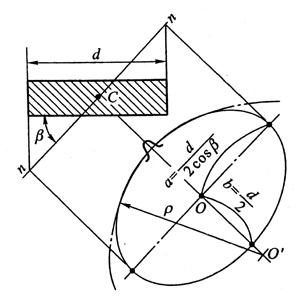
其中上图中的椭圆为实际齿轮，与椭圆相切的圆为当量齿轮，由计算得ρ = a²/b = d/2cos²β

• ①因此该当量齿轮的当量齿数zv = 2ρ/mn = z/cos³β
• ②在判断是否根切时，需要运用到这个概念

  几何尺寸计算

名称	代号	计算公式	备注
端面模数	mt	mt=mncosβ	mn根据强度计算或结构需要而定
螺旋角	β	β一般取10°到25°
齿数	z	根据强度计算或结构需要而定
当量齿数	zv	zv=z/cos³β
中心距	a	a=mt(z1+z2)/2
端面压力角	αt	tan(αt)=tan(αn)/cosβ	αn为标准值
分度圆直径	d	d1=mtz1,d2=mtz2
法向齿距	pn	pn=πm	分度圆上
端面齿距	pt	pt=πm/cosβ	分度圆上
齿厚	s	p=πmt/2	分度圆上
齿槽宽	e	p=πmt/2	分度圆上
基圆直径	db	db=dcosα=mtzcosα
基圆齿距	pb	pb=πmtcosα=mtzcosα
齿顶圆直径	da	da=mn(z+2)
齿根圆直径	df	df=mn(z-2.5)
齿顶高	ha	ha=han❀×mn=mnn	han❀为标准值=1
齿根高	hf	hf=（han❀+cn❀）mn=1.25mn	cn❀为标准值=0.25

• 注：β=0时，即为直齿圆柱齿轮

直齿锥齿轮

基本概念

1.直齿锥齿轮齿廓曲面的形成与直齿圆柱齿轮相似。如左图所示，当一扇形发生面S在基圆锥上作纯滚动时，发生面上过锥顶0的线段KK’所形成的轨迹AA’K’K即为锥齿轮的齿廓曲面。

2.因发生面沿基圆锥作纯滚动时，过0点的直线KK’上的K点至锥顶0点的距离不变，因此渐开线AK是在以点0为球心、OK为半径的球面上，故称渐开线AK为球面渐开线。

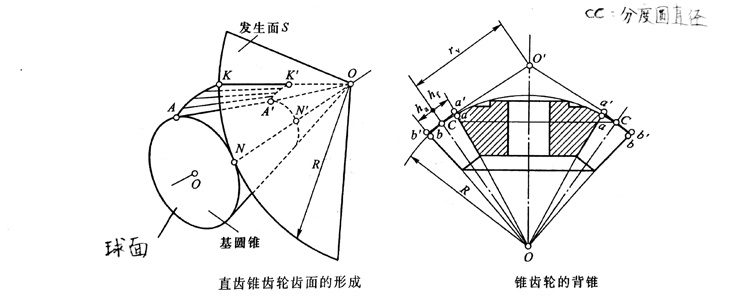
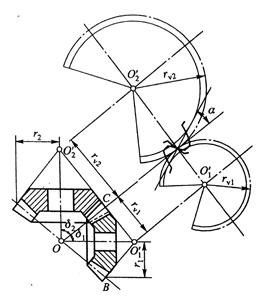
3.将背锥表面展开为一扇平面，以背锥锥矩rv为分度圆半径，补足为完整的直齿圆柱齿轮，齿数增加至zv1，这个直齿圆柱齿轮就是锥齿轮的当量齿轮。zv1为当量齿数。其中Zv1 = Z1 / cosδ1

等顶隙收缩齿轮

1.下图左所示锥齿轮副，其两轮的顶锥、根锥与分度圆锥的锥顶点重合，齿顶间隙沿齿宽方向不相等，称为不等顶隙收缩齿锥齿轮传动。

2.而下图右所示两轮的根锥仍与分度圆锥的顶点重合，但两轮顶锥的顶点不再与分度圆锥的顶点重合，而是一轮的顶锥母线与另一轮的根锥母线平行，所以在整个齿宽方向齿顶间隙不变，故称为等顶隙收缩齿轮传动。

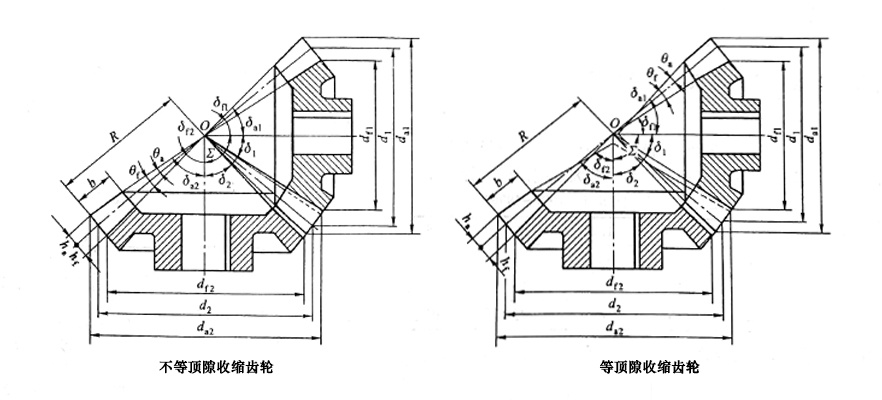
3.等顶隙收缩齿锥齿轮传动的优点是，能加大齿根和刀具的圆角半径，提高齿轮的弯曲强度和刀具的寿命有助于避免小端齿顶变尖等顶隙有利于齿轮的润滑等。因此其应用日益广泛。