机械设计笔记
主要讲了一些机械零件的选型计算。老师上复习课的时候说了下要记忆的公式,然后考了90%……
注:基于武汉理工大学MOOC、《机械原理与机械设计》(ISBN:9787040402827)
机械设计需要记忆的公式汇总
机械设计基础
- $\psi_\sigma$ 材料受循环正应力时的材料特性系数
- $\sigma_{-1},\sigma_0$ 循环特征值 r 为 -1、0 时的极限应力
上面的式子可以通过 在极限应力图中AD段方程求解化简 得到
机械设计基础
- $S_\sigma$ 稳定变应力状态下正应力安全系数
- $\sigma_\max^{‘}$ 极限应力
- $\sigma_\max$ 危险界面上的最大应力
- $(K_\sigma)_D$ 考虑到 应力集中、表面情况和绝对尺寸 而添加的系数
其实 $\sigma_\max=(K_\sigma)_D\sigma_a+\psi_\sigma\sigma_m$ 是极限应力图中线段AD的方程(没错,又是它)
机械设计基础
- $S_\sigma,S_\tau$ 正应力、切应力安全系数
齿轮传动设计
- $\sigma_F$ 齿轮齿根弯曲疲劳应力
- $F_{t1}(N)$ 为小轮上圆周力 $F_{t1}=2000T_1(N\cdot m)/d_1(mm)$
- $Y_{Fa},Y_{Sa},Y_\epsilon$ 齿形系数、应力修正系数、重合度系数;前两个乘起来又叫做复合系数
- $K=K_AK_vK_\beta K_\alpha$
- $b,m(mm)$ 轮齿齿宽、模数
齿轮传动设计
- $\sigma_H$ 齿面接触疲劳应力
- $Z_E,Z_H,Z_\epsilon$ 弹性系数、节点区域系数、重合度系数(没错,又叫这个名字)
- $u={z_2}/{z_1}$ 其中1代表小齿轮,而非主动轮
- 外啮合取为正,内啮合取负值
- $b,d_1(mm)$ 轮齿齿宽,小齿轮直径
带传动设计
- $L$ 带轮长度
- $d_1,d_2,a$ 小带轮直径、大袋轮直径、中心距
它用了一个代换式 $\beta\approx\sin\beta= (d_2-d_1)/2a$
这个看起来很难背,其实很容易忘,话说这玩意会考?emmmmmm
带传动设计
- $F_1,F_2,f_v,\alpha$ 紧边拉力,松边拉力,当量摩擦系数,包角
著名的 欧拉公式
螺纹连接
- $F^{‘}$ 预紧力
- 适用于轴向不受工作载荷的紧螺栓连接
- $K_f,F_R,f,m$ 可靠性系数,横向工作载荷,摩擦系数,结合面数量
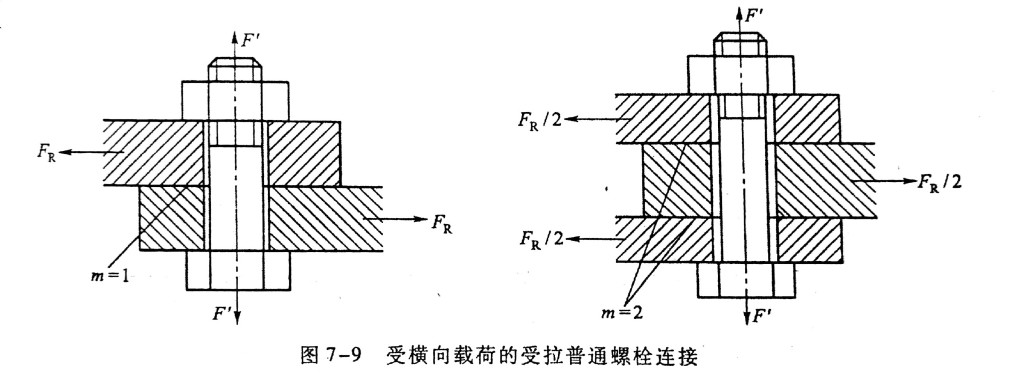
波波说要知道这个式子的物理意义。
这个式子是为了防止被连接件之间发生相对滑动,结合面之间的摩擦必须大于横向载荷得来的。
当收到轴向载荷时,上式的 F‘ 应该为 F’’
螺纹连接
- $F_0,F,F^{‘},F^{‘’}$ 总拉力、轴向工作载荷、预紧力、剩余预紧力
- 适用于轴向受工作载荷的紧螺纹连接
- 详细解释见下图,其中$C_1=\tan\theta_1,C_2=\tan\theta_2$
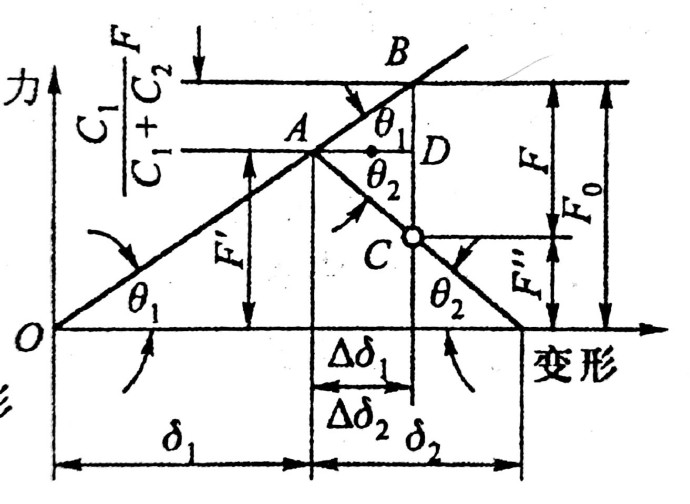
螺纹连接
- $\sigma_a$ 受轴向变载荷螺栓的应力幅
- 相关参数在前面
- $\frac{C_1}{C_1+C_2}$ 是螺栓的相对刚度,为了提高螺栓的承载能力,应该使这个值尽可能小
- $\frac{C_2}{C_1+C_2}$ 是被连接件的相对刚度,为了提高螺栓的承载能力,应该使这个值尽可能大
螺纹连接
- 无论受不受轴向载荷,对受拉轴承都适用
- $\sigma_{ca}$ 为复合拉应力
- $d_1(mm)$ 为螺纹小径
$1.3$:在用 第四强度理论 对 大量螺栓 进行 统计分析 时发现,其复合拉应力的计算只需要将拉伸应力 $\sigma$ 扩大30%来考虑扭矩的影响(就是说,切应力懒得算了,直接把正应力扩大30%,得到的效果和算切应力是一样的)
波波让我们背的是这个:$d_1\geq\sqrt{\frac{4\times1.3F^{‘}}{\pi[\sigma]}}$ 这个和上面那个是一样的
轴的设计
- $[\tau_T]$(MPa) 许用扭转应力
- $P(kW),n(r/\min)$ 轴所传递的功率,轴的转速
波波说注意是 三次根号 ,很多人搞错了
滑动轴承设计
- 上式为径向滑动轴承的设计计算
- $F(N),B(mm),d(mm),n(r/\min),p(MPa),v(m/s)$ 径向载荷,工作宽度、轴颈直径、转速、轴承平均压强,滑动速度
验证 $pv$ 是为了限制摩擦功耗与温升
滑动轴承设计
- 计算流体动压润滑轴承的基本方程
- $\eta$ 流体粘度
- $v$ 流体速度
- $h$ 任意处油膜厚度
- $h_0$ 当 $p=p_\max$ 时的油膜厚度
这。。。这玩意会考?×2
滑动轴承设计
- $F$ 液体摩擦径向滑动轴承所能承受的径向载荷
- $C_p$ 承载量系数,与长径比 B/d 有关
- $\psi=(R-r)/r$ 相对间隙。相对间隙大,轴的承载能力小。设计时根据载荷和速度选取($v\uparrow,F\downarrow\Rightarrow\psi\uparrow$)
- $B$ 工作宽度
滚动轴承及其装置设计
- $P$ 滚动轴承当量动载荷
- $X,Y$ 径向动载荷系数,轴向动载荷系数
- $f_P$ 冲击载荷系数
滚动轴承及其装置设计
- $L_h(h)$ 轴承寿命
- $C$ 基本额定动载荷
- $f_t$ 温度系数
- $\varepsilon$ 寿命系数,球轴承 $\varepsilon=3$ ,滚子轴承 $\varepsilon=10/3$
- $n(r/\min)$ 转速
- $P(N)$ 当量动载荷
轴向力判断方法
- 判明轴上全部轴向力(包括外载荷 $F_A$ 和内部轴向力 $F_S$),合力指向,确定
压紧端和放松端 压紧端轴向力 = ∑所有轴向力(除自身内部轴向力外)放松端轴向力 = 自身轴向力
内部轴向力
方向:使内外圈脱离的方向,即由小口指向大口
大小:
| 轴承类型 | 角接触球轴承C | 角接触球轴承AC | 角接触球轴承B | 圆锥滚子轴承 |
|---|---|---|---|---|
| $F_S$ | $0.5F_r$ | $0.7F_r$ | $1.1F_r$ | $F_r/(2Y)$ |
2018©Fu_Qingchen
[参考资料]:冯雪梅,李波,韩少军.机械原理与机械设计.北京高等教育出版社.2014
[图片来源]:冯雪梅,李波,韩少军.机械原理与机械设计.北京高等教育出版社.2014[拍摄]
| 名称 | 主要参数 | 选用参数 | 主要破坏形式 | 计算准则 |
|---|---|---|---|---|
| 软齿面齿轮 | m,z | m,z | 齿面点蚀 | 按齿面接触疲劳强度计算;按齿根弯曲疲劳强度校核 |
| 硬齿面齿轮 | m,z | m,z | 轮齿折断 | 按齿根弯曲疲劳强度计算;按齿面接触疲劳强度校核 |
| 蜗杆 | $m,\alpha,z,d,q,\gamma$ | m,d1,q | 胶合、点蚀、磨损 | 只按齿面接触疲劳强度计算;常常需要计算效率、验算热平衡 |
标准件带 |
$a,d,L,\alpha$ | P,n | 打滑、疲劳破坏 | 保证带传动不打滑的前提下,充分发挥带的传动能力(算有效拉力极限值) |
标准件链 |
链节距p | ? | 铰链磨损、疲劳破坏 | 高速按功率曲线计算;低速按静强度计算; |
标准件键 |
l,b,h | 轴径、轮毂长 | 压溃、磨损 | 强度校核 |
| 螺纹 | 比较多 | ? | 断裂、压溃或剪断 | 受拉螺栓为静力或疲劳拉力计算 |
机械设计基础
机械设计研究内容:机械零件的工作原理、选用、设计和计算。
本章是重点,本章的重点有:安全系数法求疲劳极限
机械零件的工作能力及失效
机械零件的工作能力
在一定的运动、载荷和环境情况下,在预定的使用期限内,不发生失效的安全工作限度
表现在强度、刚度、耐磨性、振动稳定性等方面
机械零件的失效
零件失去了工作能力
- 断裂:分为过载断裂(工作应力超过材料的强度极限)、疲劳断裂(工作一段时间之后,交变应力超过疲劳极限引起无征兆的断裂)
- 变形:分为塑性变形、过大的弹性变形
机床上加工零件的主轴就有这方面的要求 - 表面失效:压溃、过度磨损「表面的压应力过大,使表面变形」,表面疲劳损坏「表面接触应力过大」,胶合「工作温度 过高引起」、腐蚀
机械零件的计算准则
用于计算并确定零件的基本尺寸的主要依据
强度准则
针对零件断裂、塑形变形或表面疲劳、损坏失效。基本上每个零件都涉及到。
计算准则为:
$\sigma\leq[\sigma]$,$\tau\leq[\tau]$,$\sigma_H\leq[\sigma_H]$(表面疲劳损坏)
其中对于线接触的情况,接触应力可以由以下公式计算:
这个公式在 齿轮 部分会再次出现,这里就不解释了
刚度准则性
非重点针对大弹性变形
计算准则为:
$y\leq[y],\theta\leq[\theta],\phi\leq[\phi]$(分别为挠度、偏转角、扭转角)
耐磨性准则
非重点针对过度磨损,验算式子为:$p\leq[p]$
振动和噪音准则
非重点针对高速机械的振动失稳(共振),防止共振条件为:$f_p\leq0.87f$ 或 $f_p\geq1.18f$(f为零件固有频率,fp为零件收振源作用引起的被迫振动频率)
可靠性准则
变应力及表达
载荷和应力的类型是按照是否变化而分类的,因此,有两种。
- 静载荷(大小与方向都不随时间变化的载荷)与变载荷(大小或方向随时间变化的载荷)
- 静应力(大小与方向都不随时间变化的载荷或极其缓慢)与变应力(大小或方向随时间变化的量)
机械零件一般都是变应力。。。
为了描述变应力这里有一些参数
变应力参数
一般来说变应力是正弦变化的,因此我们可以把应力这样画出来:
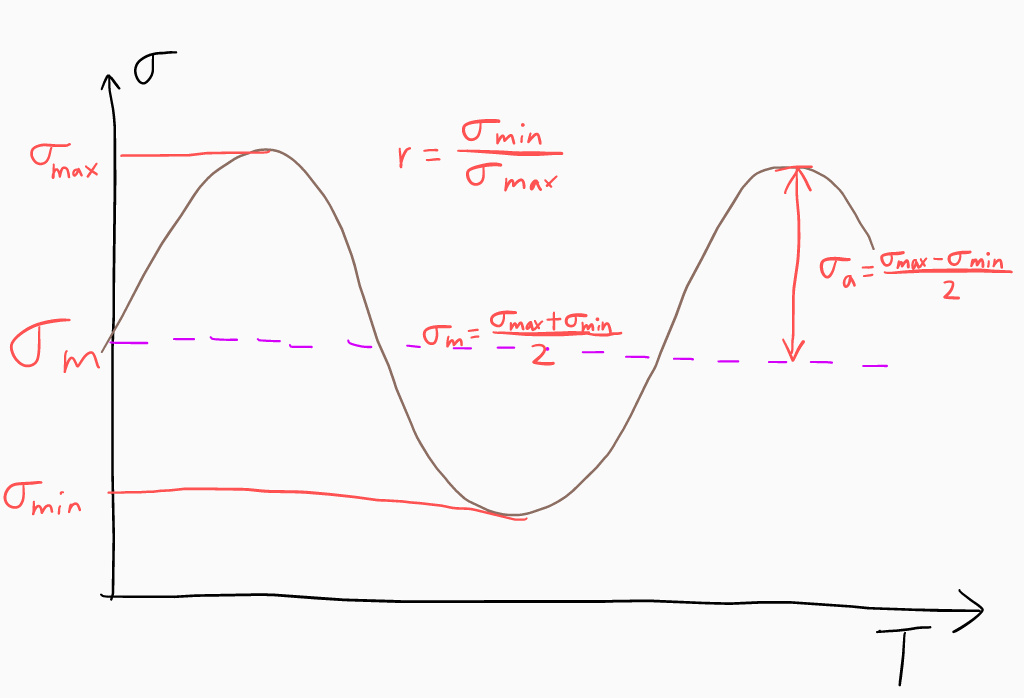
可以发现有一些关键的数据:
最大应力 $\sigma_{max}$、最小应力 $\sigma_{min}$
平均应力$\sigma_{m}=\frac{\sigma_{max}+\sigma_{min}}{2}$、应力$\sigma_{a}=\frac{\sigma_{max}-\sigma_{min}}{2}$
循环特征 $r = \frac{\sigma_{min}}{\sigma_{max}}$(易得,$-1\leq r\leq1$)
然后呢有一些比较有名的特例,在后面也比较常见。
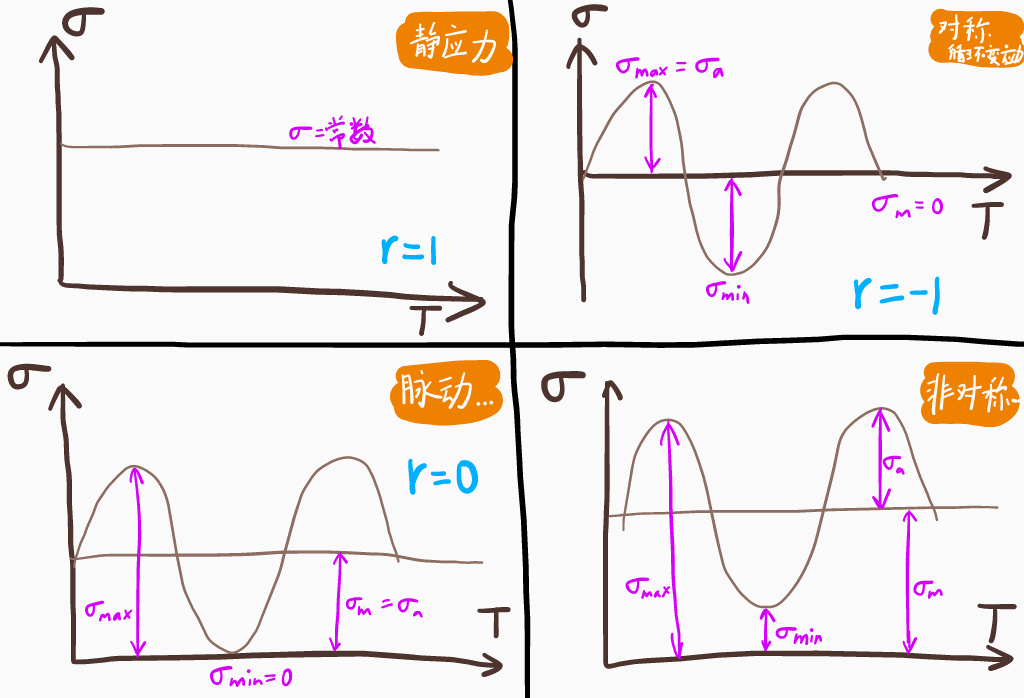
机械零件的疲劳极限
【本章重点】满足强度要求是机械最基本的要求,然后强度又分为静应力强度和变应力强度,然后机械中最常见的又是变应力。。。
疲劳损坏机理
先来研究一下这个,看看疲劳极限有什么东西有关:
变应力作用下的疲劳断裂有一下过程:零件表面应力超过极限值→微裂纹→扩展→裂纹
根据以往的经验,疲劳极限除了与 材料 有关,还与 循环特征 r、应力循环次数 N、应力集中、绝对尺寸及表面状态有关。
疲劳极限
知道了疲劳极限与什么有关之后就要开始求了。根据应力疲劳试验有以下图形:
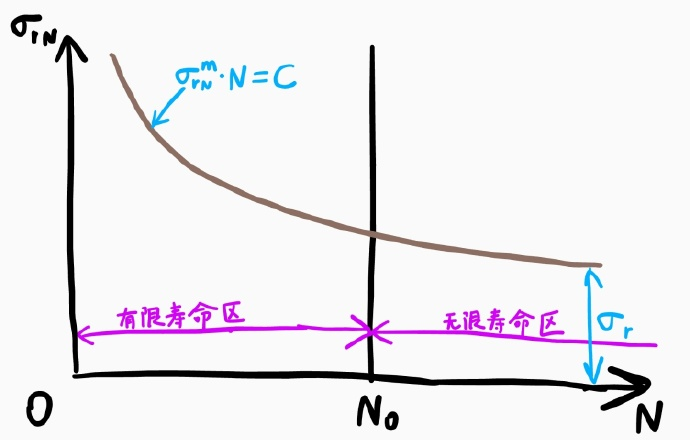
对上图,一般取一个 规定 的 $N_0$,有一个对应的 $\sigma_r$,这个值就是材料的疲劳极限(也就是无限寿命疲劳极限)。
研究无限寿命区的疲劳极限没有意义(都无限寿命了就没极限了),有限寿命区的疲劳极限由图形可以得到:
然而这个只能得到一种循环特征 r下的疲劳极限,而且应力疲劳试验做起来成本比较高。对每个 r 都做试验然后得到上面的式子显然不实际。极限应力图 解决了这个问题,工程上也常常用这个图来近似代替。
极限应力图
以 $\sigma_a$ 为纵坐标,$\sigma_m$ 为横坐标,即可做出任意材料的极限应力图。工程上一般先测出 对称循环 和 脉动循环 的疲劳极限为 $\sigma_{-1},\sigma_{0}$,此时可以在图上画出3个点(静力点 $(\sigma_s,0)$、对称循环 $(0,\sigma_{-1})$、脉动循环 $(\sigma_0/2,\sigma_0/2)$)。根据这三个点,按照下图,即可画出由两条直线构成的曲线。这个曲线叫做 简化极限应力曲线
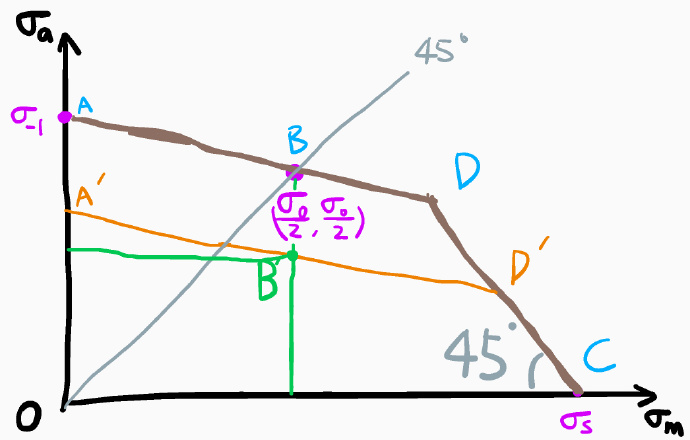
这个曲线不但可以使用很少的已知数据 $(\sigma_{-1},\sigma_0,\sigma_s)$ 画出,而且能够满足设计的需要。
其中:
AD段方程为:$\sigma_a^{‘} = \sigma_{-1}+\sigma_m^{‘}\times\frac{\frac{\sigma_0}{2}-\sigma_{-1}}{\frac{\sigma_0}{2}}\Rightarrow\sigma_{-1}=\sigma_a^{‘}+\sigma_m^{‘}\times\psi_\sigma$
CD段方程为:$\sigma_s=\sigma_a^{‘}+\sigma_m^{‘}$
$r_D=\frac{\sigma_{-1}(\sigma_s-\sigma_0)}{\sigma_s(\sigma_0-\sigma_{-1})}$
其中,$\psi_\sigma=\frac{2\sigma_{-1}-\sigma_0}{\sigma_0}$ 为材料特性系数(课本)或等效系数(PPT)
对于工作应力为$(\sigma_a,\sigma_m)$的一点来说:
其应力循环特征 $r=\frac{\sigma_{\min}}{\sigma_{\max}}=\frac{\sigma_m-\sigma_a}{\sigma_m+\sigma_a}=\frac{1-\frac{\sigma_a}{\sigma_m}}{1+\frac{\sigma_a}{\sigma_m}}=\frac{1-\tan\alpha}{1+\tan\alpha}$
对应的疲劳极限 $\sigma_{\max}^{‘}=\sigma_m^{‘}+\sigma_a^{‘}$,与上方AD或CD段联立方程即可解出疲劳极限。
不过,以上内容并没有讨论应力集中、绝对尺寸及表面状态 对疲劳极限的影响。由于以上问题比较复杂,因此在工程中,使用 $(K_\sigma)_ D$ 来代替这些因素的影响。这样的话极限应力图就有了一些变化,就变成了曲线 A’B’D’C’
A’B’、C’D’段,需要将纵坐标 $\sigma_{-1},\sigma_0$ 替换为 $\frac{\sigma_{-1}}{(K_\sigma)_ D},\frac{\sigma_0}{(K_\sigma)_ D}$
此时:
AD段方程为:$\sigma_{-1}=(K_\sigma)_ D\sigma_a^{‘}+\psi_\sigma\sigma_m^{‘}$
CD段方程为:$\sigma_s=\sigma_a^{‘}+\sigma_m^{‘}$
然后上面还没有讨论切应力。切应力和正应力一样,只是需要将上面式中的 $\sigma$ 替换成 $\tau$
上面求出了极限应力的值,然后通常还要求 安全系数
这个比较麻烦,然后我也忘记当时是怎么讲的了,直接给出结论:
在 单向应力 作用下
在 复合应力 作用下
机械中的摩擦、磨损和润滑
这一部分内容是抄的MOOC上面的
摩擦
| 类型 | 解释 | 摩擦系数 |
|---|---|---|
| 干摩擦 | 表面间无任何润滑剂或保护膜的纯金属接触时的摩擦 | 大于0.1 |
| 边界摩擦 | 表面间被极薄的润滑膜所隔开,且摩擦性质与润滑剂的粘度无关而取决于两表面的特性和润滑油油性的摩擦 | 0.01-0.1 |
| 流体摩擦 | 表面间的润滑膜把摩擦副完全隔开,摩擦力的大小取决于流体分子内部摩擦力的摩擦 | 0.001-0.008 |
| 混合摩擦 | 摩擦副处于干摩擦、边界摩擦和流体摩擦混合状态时的摩擦 | - |
磨损
由于表面的相对运动而使物体工作表面的物质不断损失的现象。
零件的磨损过程大体可分为三个阶段:磨合磨损阶段、稳定磨损阶段及剧烈磨损阶段
| 类型 | 解释 |
|---|---|
| 表面疲劳磨损 | 摩擦表面受循环接触应力作用到达一定程度时,就会在零件工作表面形成疲劳裂纹,随着裂纹的扩展与相互连接,会造成许多微粒从零件表面上脱落下来,致使表面上出现许多浅坑,这种磨损过程即为疲劳磨损; |
| 粘着磨损 | 摩擦表面的微凸体在相互作用的各点发生粘着作用,使材料由一表面转移到另一表面的磨损 |
| 磨粒磨损 | 摩擦表面间的游离硬颗粒或硬的微凸体峰间在较软的材料表面上犁刨出很多沟纹的微切削过程 |
| 腐蚀磨损 | 在摩擦过程中金属与周围介质发生化学反应而引起的磨损。 |
润滑
润滑的作用有:减少或防止磨损、降低温升、防锈、降低摩擦、缓冲和吸振
润滑的原理会在后面介绍
齿轮传动设计
齿轮主参数:m、z
本章的重点为强度计算以及载荷系数
齿轮的特点与分类
特点
优点:瞬时传动比恒定、传动效率高、工作使用效率高、结构紧凑、适用范围大
缺点:成本高、精度低时噪音大,不易用于间距过大的转动
分类
- 按照齿轮的工作条件:闭式、开式、半开式
- 按照齿面硬度分:软齿面(HB ≤ 350)、硬齿面(HB > 350)
齿轮的主要失效形式和计算准则
齿轮的主要失效形式
齿轮的折断
闭式齿轮当齿轮的齿面比较硬的时候容易发生
- 疲劳折断:齿根应力集中、交变载荷反复作用、疲劳裂纹拓展
- 脆性折断:齿轮脆性材料、冲击、过载
防止措施:增大齿根厚度、加工精度、选择合理材料、材料热处理、增大心部韧性
疲劳断裂往往从齿根受拉处开始发生
齿面的疲劳点蚀
闭式齿轮传动的主要失效形式,软齿面上容易发生。
- 点蚀原因:接触应力的反复作用
- 后果:渐开线被破坏,产生噪音,甚至不能工作
防止措施:增大齿面硬度、降低粗糙度、合理选择润滑油
点蚀主要出现在节线附近的齿根表面上
齿面磨损
开式齿轮传动主要失效形式
- 原因:齿面有磨料存在
- 后果:齿面破坏、引起冲击振动
防止措施:改善润滑、提高齿面硬度、改用闭式齿轮传动
齿面胶合
胶合现象是指两表面尖峰接触后粘接,然后再被撕开。 高速重载 齿轮容易发生
- 原因:齿面软、相对滑动速度高、温度高、润滑失效
- 后果:与上面类似
防止措施:改善润滑条件、提高齿面硬度、降低齿面粗糙度
塑性变形
有两种:齿体塑性变形(歪了)、齿面塑性变形(齿面材料沿摩擦力反向流动)
- 原因:齿面软、润滑失效
防止措施:提高齿面硬度、提高润滑粘度
| 类型 | 原因 | 防止措施 |
|---|---|---|
| 轮齿的折断 | 疲劳折断:齿根应力集中、交变载荷反复作用、疲劳裂纹拓展 脆性折断:齿轮脆性材料、冲击、过载 | 增大齿根厚度、加工精度、选择合理材料、材料热处理、增大心部韧性 |
| 齿面点蚀 | 接触应力的反复作用 | 增大齿面硬度、降低粗糙度、合理选择润滑油 |
| 齿面磨损 | 齿面有磨料存在 | 改善润滑、提高齿面硬度、改用闭式齿轮传动 |
| 齿面胶合 | 齿面软、相对滑动速度高、温度高、润滑失效 | 改善润滑条件、提高齿面硬度、降低齿面粗糙度 |
| 塑性变形 | 齿面软、润滑失效 | 提高齿面硬度、提高润滑粘度 |
齿轮传动设计准则
| 齿轮类型 | 主要失效形式 | 设计准则 | 校核准则 |
|---|---|---|---|
| 闭式软齿面 | 齿面点蚀 | 齿面接触疲劳强度 | 齿根弯曲疲劳强度 |
| 闭式硬齿面 | 轮齿折断 | 齿根弯曲疲劳强度 | 齿面接触疲劳强度 |
| 开式齿轮 | 齿面磨损 | 多按齿面弯曲疲劳强度 | ? |
齿轮材料与热处理
要求
内软外硬、良好的机械加工和热处理、价格低
常用材料
锻钢(最常用)、铸钢(比较大的齿轮)、铸铁(速度低,功率不大的齿轮)、有色金属(常用于化工、医疗方面)
齿轮传动的计算载荷
计算载荷:名义载荷 × 载荷系数
载荷系数: $K = K_AK_vK_\beta K_\alpha$
使用系数 $K_A$
考虑到 外部因素 (冲击振动)引起的附加动载荷影响的系数
与 原动机与工作机的工作状态 有关
动载系数 $K_v$
考虑到 齿轮本身的制造精度、运转速度 引起的附加动载荷影响的系数(齿轮齿距不相等→齿轮啮合时齿面有冲击载荷)
与 齿轮速度、齿形误差、轮齿啮合刚度 有关(精度↑,速度↓ → $K_v$↓;齿轮心部刚度↓ → 变形↑ → 间隙↓ → 载荷分布均匀)
减少影响:提高精度、齿廓修形
齿向载荷分布系数 $K_\beta$
考虑到轴安装的过程中轴的误差(轴装歪了),以及变形引起的载荷分布不均匀现象的影响系数
当齿宽较小、齿轮轴刚度较大,齿面较软,齿轮对称布置时,$K_\beta$ 较小(齿面越软,接触越多)
齿间载荷分布系数 $K_\alpha$
考虑到 单齿啮合和多齿啮合载荷分布不均匀 对的影响的系数
影响其因素有:重合度、齿轮刚度(齿面硬,数值大)、齿面精度
| 名称 | 引起原因 | 影响因素 |
|---|---|---|
| 使用系数 $K_a$ | 外部因素(如冲击、振动) | 原动机和工作机的工作状态 |
| 动载系数 $K_v$ | 齿轮本身的制造误差、运转速度使啮合时齿间产生冲击造成附加动载 | 制造精度、运转速度、齿轮啮合刚度(越大越不均匀) |
| 齿向载荷分布系数 $K_\beta$ | 由于轴的安装误差和轴、轴承的变形(轴歪了)等引起的载荷分布不均匀 | 轴的刚度、齿面硬度、齿宽(越大越不均匀) |
| 齿间载荷分布系数 $K_\alpha$ | 单齿啮合和多齿啮合引起的载荷分布不均匀 | 重合度、齿轮精度、齿面硬度 |
斜齿轮传动十分平稳,因此 K 比圆柱齿轮小;锥齿轮设计误差和制造误差大,因此 K 比圆柱齿轮大
齿轮的结构设计
结构设计要考虑齿轮的几何尺寸、毛坯材料、加工工艺、使用等因素。通常是先按照齿轮的直径大小,选择合适的结构形式然后再根据经验数据完成结构设计。常用的结构形式有齿轮轴、实心式齿轮、腹板式齿轮、轮辐式齿轮、组装齿卷式结构等等。
注:选择的范围并不是特别的严格
齿轮轴
齿轮和轴做成一体的轴。
当圆柱齿轮齿根圆到键槽底面的径向距离 $e\leq2.5 m(m_n)$,要制作成齿轮轴。

制作成这样的原因是很难做出来,即使制作出来轮毂的强度也不够。
实心式齿轮
最基本最简单的齿轮。
当 $d_a\leq200mm$ 且 $e\geq 2.5m(m_n)$ 时,做成实心式齿轮。
腹板式齿轮
当 $200mm\leq d_a \leq 500mm$ 时,通常采用腹板式齿轮。
目的是减少质量、节约材料。
轮辐式齿轮
$d_a=400\sim1000mm$ 时,采用轮辐式铸造结构。
目的还是减少质量、节约材料。
镶套式齿轮
当齿轮要使用比较好的材料时,可以将齿圈用好材料;齿轮本体用差的材料两者镶套起来的叫做嵌套式齿轮。
好处是:节约材料,而且当齿轮磨损之后也只用更换齿圈。
焊接式齿轮
用钢板焊接出来的齿轮。
适用于单件生产、尺寸过大又不利于铸造的齿轮
缺点是有焊接内应力
受力分析
直齿圆柱齿轮
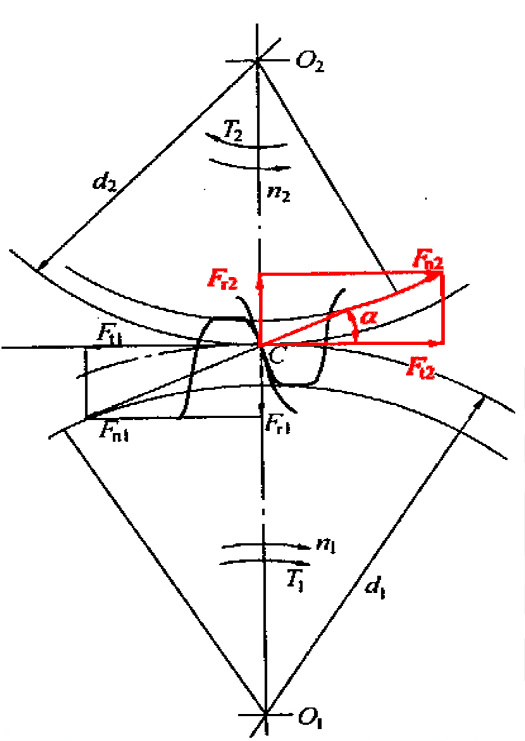
| 名称 | 计算公式 | 方向 |
|---|---|---|
| 圆周力 $F_t$ (tangential) | $F_t=2T_1/d_1$ | 主反从同 |
| 径向力 $F_r$ (radial) | $Fr=F_t\tan\alpha$ | 指向圆心 |
| 法向力 $F_n$ (normal) | $F_n=F_t/\cos\alpha$ | 前两个矢量和成 |
(其中T1=9548·P/n为小齿轮扭矩;d1为小齿轮节圆直径,SI)
斜齿圆柱齿轮
| 名称 | 计算公式 | 方向 |
|---|---|---|
| 圆周力 $F_t$ | $F_t=2T_1/d_1$ | 主反从同 |
| 径向力 $F_r$ | $F_r=F_t\tan\alpha_n/\cos\beta$ | 指向圆心 |
| 法向力 $F_n$ | $F_n=F_t/(\cos\alpha_n\cos\beta)$ | 合成 |
| 轴向力 $F_a$ | $F_a=F_t\tan\beta$ | 主动轮右手定则(四指为旋转方向,大拇指为受力方向) |
齿轮齿面接触疲劳强度
直齿圆柱齿轮
$\propto$ 接触应力、齿轮材料许用接触应力
齿轮轮齿节线接触为体接触,此时运用 赫兹公式
$F_n(N)$ :正压力
- 计算载荷为$F_{nc}=KF_n=\frac{KF_t}{\cos\alpha}$
$L(mm)$ :接触线长度$L=b_r=\frac{b}{Z_\varepsilon^2}$
其中$b_r$为有效齿宽,$Z_\varepsilon$为直齿轮重合度系数
$\rho_\Sigma(mm)$ :综合曲率半径$\frac{1}{\rho_\Sigma}=\frac{1}{\rho_1}\pm\frac{1}{\rho_2}$
其中 $\rho=\frac{d}{2}\sin\alpha$ (就是基圆半径)
令$\frac{d_2}{d_1}=\frac{Z_2}{Z_1}=u$,则$\frac{1}{\rho_\Sigma}=\frac{2}{d_1\cos\alpha\tan\alpha^{‘} }\frac{u\pm1}{u}$
其中,令$Z_H=\sqrt {\frac{2}{\cos^2\alpha\tan\alpha^{‘} } }$,记为节点区域系数
$(\pm)$ :外接触取正号,内接触取负号
$Z_E(\sqrt{MPa})$ :材料弹性系数$Z_E=\sqrt{\frac{1}{\pi(\frac{1-\mu_1^2}{E_1}+\frac{1-\mu_2^2}{E_2})} }$
其中 E 为弹性模量,μ 为泊松比
经过整理,可得齿面接触疲劳强度的校核公式
| 名称 | 计算式 | 影响因素 |
|---|---|---|
| 材料弹性系数 $Z_E$ | $Z_E=\sqrt{1/[{\pi(\frac{1-\mu_1^2}{E_1}+\frac{1-\mu_2^2}{E_2})}]}$ | 弹性模量、柏松比 |
| 节点区域系数 $Z_H$ | $Z_H=\sqrt{4/\sin{2\alpha}}$ | 节点处齿廓曲率 |
| 直齿轮重合度系数 $Z_\varepsilon$ | $Z_\varepsilon=\sqrt{(4-\varepsilon_a)/3}$ | 重合度 |
| 齿宽系数 $\psi_d$ | $\psi_d=b/d_1$ | - |
大齿轮与小齿轮应力相同,但许用应力不一定相同。
式中:u 是 齿数比 $u=z_2/z_1$,u > 1(1为小齿轮,2为大齿轮)
斜齿圆柱齿轮
斜齿轮和直齿轮差不多,就是多了一个系数。
注:查表时使用 当量齿数
| 名称 | 计算式 | 影响因素 |
|---|---|---|
| 螺旋角系数 $Y_\beta$ | $Z_\beta=\sqrt{\cos\beta}$ | 螺旋角 |
齿轮齿根弯曲强度
直齿圆柱齿轮
计算齿根弯曲强度时将齿根当做悬臂梁,计算得出。
首先是判断危险界面
30°切线法
作与轮齿轴线成30°角的直线与齿轮圆角过渡曲线相切,过两切点并垂直于轴线的面就是危险截面
计算公式
| 名称 | 说明 |
|---|---|
| 齿形系数 $Y_F$ | 考虑到轮齿几何形状对齿根弯曲应力的影响。决定于齿数,与模数无关。 |
| 应力修正系数 $Y_S$ | 考虑到齿轮过渡圆角处应力集中和剪切应力及压应力对齿根应力影响 |
| 重合度系数 $Y_\varepsilon$ | 顾名思义 |
注:大齿轮与小齿轮是不同的
斜齿圆柱齿轮
按照发面当量圆柱齿轮计算。然后也是多了一个系数
然后注意:模数为法向模数,查表采用 当量齿数
锥齿轮相关
标准参数在大端,不考虑与重合度相关的因素($K_\varepsilon,Z_\varepsilon,Y_\varepsilon$),按当量齿数 $z_v=z/\cos\delta_1$ 查表。
受力分析
| 名称 | 相关公式 | 方向 |
|---|---|---|
| 圆周力 $F_t$ | $F_{t1}=-F_{t2}$ | 主反从同 |
| 径向力 $F_r$ | $F_{r1}=-F_{a2}$ | 指向圆心 |
| 轴向力 $F_a$ | $F_{a1}=-F_{r2}$ | 指向大端 |
载荷系数
$K=K_AK_vK_\beta$
齿面接触疲劳强度
其中 Zk 为锥齿轮增加的一个系数
齿轮传动的润滑
润滑可以起到减小啮合处的 摩擦发热、减少磨损、降低噪音 的作用
| 传动方式 | 速度 | 润滑方式 |
|---|---|---|
| 开式及半开式齿轮 | 低 | 人工定期润滑或润脂 |
| 闭式齿轮 | <10m/s | 浸油润滑 |
| 闭式齿轮 | ≥10m/s | 喷油润滑 |
齿轮传动主要参数
模数:主要影响 齿根弯曲强度,可以按照齿根弯曲疲劳强度计算
齿数:齿数多,传动平稳。需要为质数
如果不互质,相互啮合的齿总是确定的,这样的话磨损位置相同,会加速磨损
蜗杆传动
- 大题预定
- 标准件,选择型号即可
蜗杆传动的特点
蜗杆最重要的一个特性就是 传动效率低。因此有自锁性等优点,也会有摩擦发热的现象(因此后面有热平衡计算)
蜗杆与蜗轮在节点处速度方向相互垂直。节点处速度 $v_s=\sqrt{v_1^2+v_2^2}$ 比较大。因此传动相对滑动大,效率低,传动磨损也比较大。
由于蜗轮蜗杆的自锁性,因此只能蜗杆带动蜗轮
蜗杆传动的失效形式、设计准则、材料
失效形式:(与齿轮类似)齿面胶合、齿面点蚀、齿面磨损,而且通常发生在蜗轮上
设计准则
| 类别 | 失效形式 | 设计准则 |
|---|---|---|
| 闭式 | 磨损 | 按齿面接触疲劳强度计算,齿根弯曲疲劳强度 校核 |
| 开式 | 磨损 | 以保证齿根弯曲疲劳强度为设计准则 |
常用的材料
不仅要求强度和刚度,还要求一定的耐磨性、减摩性和跑和性
- 蜗杆常用碳素钢或合金钢
- 蜗轮铸铁、铸造青铜等等
蜗杆的效率、润滑、热平衡计算
效率
$\eta_1$:啮合效率(与蜗轮头数有关。当 $z_1 = 1$ 时,$\eta_1=0.7$)
$\eta_2,\eta_3$:轴承效率、搅油效率
$\gamma$:导程角,与斜齿轮的螺旋角比较类似
- $z_1$:蜗杆头数
- $q$:蜗杆直径系数 $q=d_1/m$(使刀具标准化)
$\rho_v$:当量摩擦角
| $z_1$ | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| $\eta$ | 0.7 | 0.8 | 0.85 | 0.9 |
头数$z_1$ 越大,加工越困难
自锁条件:$\gamma\leq\rho_v$
相对滑动速度
润滑
目的:防止 胶合(有时还会加添加剂)和 磨损
开式:定期涂润滑脂
闭式:浸油(深度为一个齿高)或喷油润滑(对准蜗杆啮入端)
热平衡计算
由于蜗杆效率低,因此工作时会产生大量的热。然而温度过高会使润滑失效,导致齿面胶合。因此需要进行热平衡计算,来保证油温在一定范围 内
单位时间的发热量为(W)
单位时间的散热量为(W)
热平衡时的油温为
一般会使 t 在80℃以下
改善散热常见的措施
- 合理设计箱体结构,焊上散热片,增大散热面积
- 在蜗轮轴上装风扇
- 在箱体油池内设置蛇形冷却水管
- 采用压力喷油循环润滑(最吼的冷却效果、润滑效果)
- 上置式:润滑效果不好,但油不易洒出来
- 下置式:润滑效果好,但油容易洒出来
蜗杆的受力分析
| 名称 | 计算公式 | 方向 |
|---|---|---|
| 圆周力 $F_t$ | $F_{t1}=-F_{a2}=2T_1/d_1$ | 主反 |
| 轴向力 $F_a$ | $F_{a1}=-F_{t2}=F_{t1}/(\cos\alpha_n\cos\gamma)$ | 左右手定则 |
| 径向力 $F_r$ | $F_{r1}=-F_{r2}=F_{t1}\tan\alpha$ | 向心 |
左旋蜗杆使用左手法则,手握蜗杆,四指指向蜗杆旋转方向,则大拇指的方向即为蜗轮在蜗杆与蜗轮啮合点的旋转方向
涡轮蜗杆的转动方向的判定方法: 主动蜗杆为右旋用右手四个手指顺着蜗杆的转向握住蜗杆,大拇指的指向与蜗轮的节点速度方向相反,来判定蜗轮的转向。
计算载荷
$K=K_AK_vK_\beta$
其中 $K_v,K_\beta$ 可以忽略
带传动
适用于中高速,常常接在原动机后面避免 超载
已标准化,只需要选择型号
带的结构与型号
- 平带
- V 带(摩擦力比平带大,传动能力强些)
V 带结构
抗拉层、顶胶层、底胶层、包布层 构成。根据抗拉层结构的不同,还分为帘布结构和线绳结构
由于带的主要成分是橡胶,因此不适合于高温、有化学腐蚀的场合
普通 V 带的型号
有 Y、Z、A、B、C、D、E 七种型号,他们的横截面积逐渐增大
中性层:当带垂直于底边弯曲时,长度保持不变的那一层。其宽度为节宽
V 带的受力分析
令带轮的初始拉力为 $F_0$,紧边拉力为 $F_1$,松边拉力为 $F_2$,有效拉力为 $F$ 有:
根据欧拉公式,当处于临界状态时,有:
此时的有效拉力为:(可以由上面式子推出)
紧边为 进入主动轮的 那一边
上式中,f 应该带当量摩擦系数,对于V带,$f_v=\frac{f}{\sin{\frac{\varphi_0}{2}}}$
增大有效拉力的方法有:增加$F_0,\alpha_1,f$
V 带的应力分析
拉应力
紧边拉应力:
送边拉应力:
由离心力产生的应力
各点处都有,且相等
这里只考虑的拉应力,原因是,其他的也拉应力,若此处考虑压应力,与其他的是相互抵消的关系
带弯曲产生的应力
- $E_b$:带的当量弯曲弹性模量
- $y_0$:带最外层到中性层距离
- $d_p$:带轮节圆直径
带的应力分布
注:最大应力产生在紧边进入小带轮处
带的弹性滑动
由于带的弹性变形而引起的带与带轮之间的相对滑动现象(不可避免的本身属性)
后果
- 使从动轮的圆周速度总是落后于主动轮的圆周速度
- 传动比不是常数
- 损失能量、降低效率、使带的温度升高,引起磨损
打滑
- 造成带的严重磨损并使带处于不稳定状态
- 打滑总是发生在小带轮处
- 打滑可以避免超载
带的失效形式与设计准则
- 失效形式:打滑和疲劳破坏
- 设计准则:$\sigma_{\max}=\sigma_1+\sigma_{b1}+\sigma_{c}\leq[\sigma]$
当 $\sigma_{\max}=[\sigma]$ 时,带发挥出最大的效能
此时,有
带的张紧
- 定期张紧装置(定期改变中心距)
- 自动张紧装置(靠重力使带张紧)
- 用带轮张紧(加一个带轮)
链传动
已标准化
套筒滚子链结构
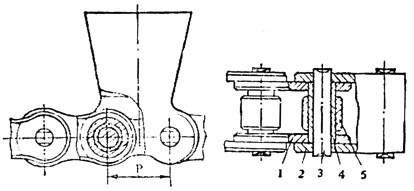
1:内链板 2:外链板 3:销轴 4:套筒 5:滚子
其中,1、4为过盈配合;2、3为过盈配合;4、5为间隙配合;3、4为间隙配合
销轴于销轴之间的距离称为 链节距 ,是链传动的主要参数
为了使链条形成环形,正好是内链板与外链板之间相连接,因此链节数最好设置成 双数
当链节数为单数时,会使用 过渡链节 来进行连接,不过强度不高,因此设计时应该尽量避免这个
链传动的不均匀性
链传动,链条会在链轮上形成一个多边形,多边形的边长就是链节距的大小。
因为形成了这种多边形,因此,其瞬时速度和瞬时传动比都是变化的,这个叫做链传动的多边形效应
链的平均速度
链的瞬时传动比
当 Z1 = Z2 时,紧边链长 = 链节距的整数倍 时,传动比 = 1,为常数
缺点
- 瞬时传动比不恒定
- 有冲击振动
- 有噪音
- 有上下分速度,有上下抖动
- 容易跳齿,容易脱链
轴毂连接设计
轮毂链接最常用的其实是 键连接
主要参数为:键宽、键高
键的主要类型
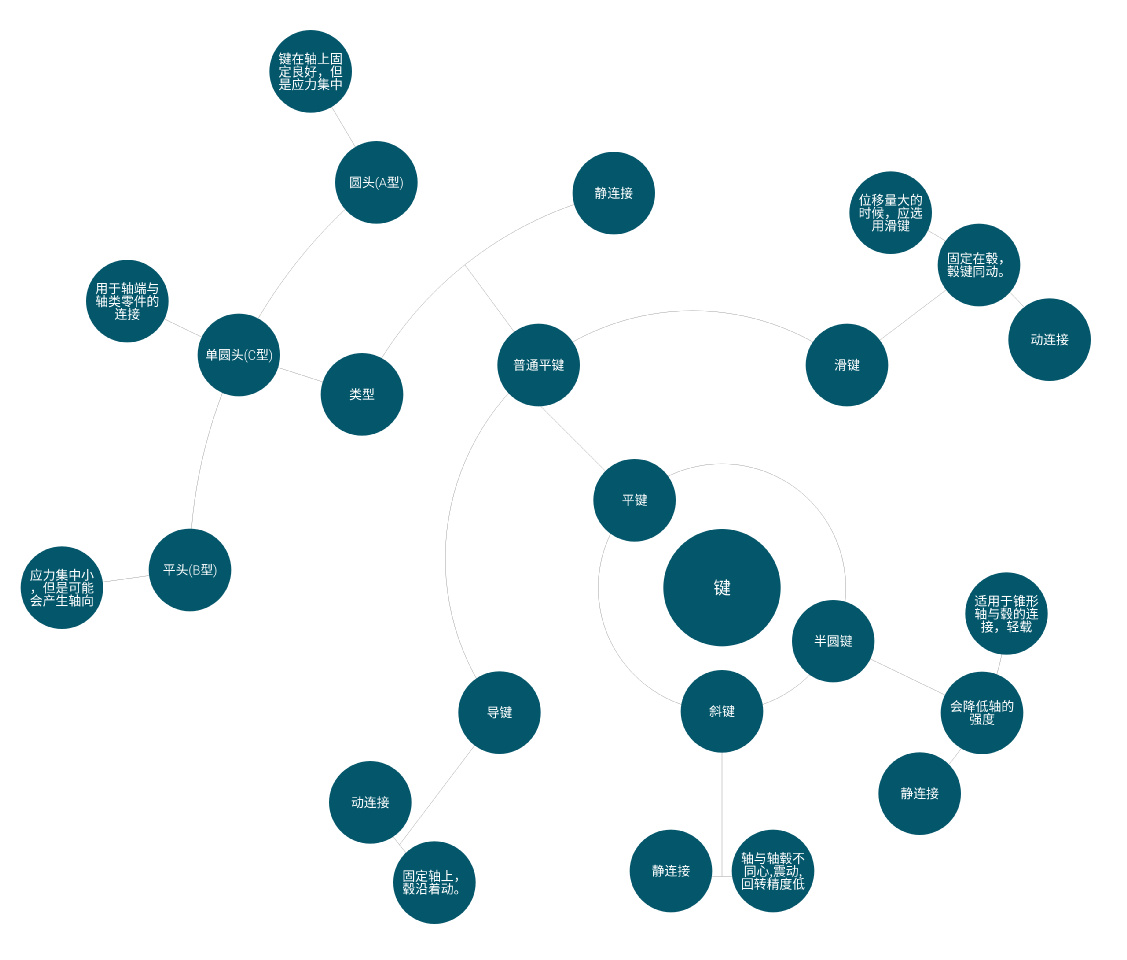
键的选择
- 键宽与键高:由轴的直径按照标准确定
- 键长:需要符合长度系列,等于或略小于轮毂长
键的强度计算
- l:键长(不含圆头)
- k:键与轮毂接触高度
- d:轴径
花键
优点
- 键槽浅,对轴的和毂的削弱小
- 载荷可以由多个齿承担,传递转矩能力强
- 对称分布,受力均匀,对中性好,旋转精度高
缺点
- 成本高
- 需要特殊的加工才能保证精度
螺纹连接
特点是结构简单、拆装方便,连接可靠性强,适用范围广
螺纹的主要参数
- 大径D:螺纹的公称直径
- 小径D1:危险界面的计算直径
- 中径D2:齿厚与齿间处相等处直径,确定几何参数
- 线速n:螺旋线的数量
- 螺距P:相邻两牙在中径线上的轴向距离
- 升角$\psi$:$\tan\psi=nP/(\pi d_2)$ 中径圆柱上螺旋展开时的角
- 牙形角$\alpha$
- 导程S:同一条螺旋线相邻两牙之间的距离
螺纹的分类
要求:足够的强度与良好性
当然各个螺纹也有自己的要求,比如说:链接螺纹(自锁性)、管螺纹(密封性)、转动螺纹(效率高)、调整螺纹(精度高)等等
普通螺纹
又叫做三角螺纹,牙形角 $\alpha=2\beta=60°$
牙形角大,当量摩擦系数大,自锁性好
根据螺距的大小,又分为粗牙螺纹和细牙螺纹
细牙螺纹螺距小,自锁性好,常用于承受冲击,振动,变载荷的地方
缺点:牙小,磨损大,易脱扣
主要用于 连接
矩形螺纹
$\alpha=\beta=0$ 传动效率高,但是加工困难,常被梯形螺纹代替
主要用于 传动
梯形螺纹
$\alpha=2\beta=30°$ 牙根强度高,易于对中,易于制造,部分螺母可以消除间隙
主要用于 传动
锯齿形螺纹
单向,效率高,牙根强度高
主要用于 传动
螺纹连接的基本类型
| 名称 | 适用范围 |
|---|---|
| 螺栓连接 | 连接件不太厚且有足够空间 |
| 螺钉连接 | 不经常拆卸的场合 |
| 双头螺柱 | 经常拆装或用螺钉无法安装 |
| 紧定螺钉 | 用于传递不大的力及扭矩,在轴上用的比较多 |
螺纹连接的预紧
预紧的目的是:增强连接的刚性,紧密型和防松能力
当然后面会有预紧力的计算
螺纹连接的防松
在静载荷作用下,螺栓连接一般能够满足自锁条件。不过当遇到 冲击振动或变载荷 时,或当温度变化很大时,摩擦副之间的摩擦力减小,可能就达不到自锁条件了,这时就会发生自动脱松现象
螺纹放松的办法有:摩擦放松、机械放松以及破坏性永久放松
| 名称 | 类别 | 备注 |
|---|---|---|
| 对顶螺母(双螺母) | 摩擦力放松 | 两个螺母对顶产生内力,增大摩擦,结构简单,但是不可靠 |
| 弹簧垫片 | 摩擦力放松 | 反弹力使螺纹将保持压紧力 |
| 锁紧螺母 | 摩擦力放松 | 螺纹旋入处镶嵌纤维或者尼龙 |
| 开口销或六角开槽螺母 | 机械放松 | - |
| 止动垫圈 | 机械放松 | - |
| 串联钢丝 | 机械放松 | 串联钢丝方向与螺钉拧紧的方向相同 |
| 焊接、冲点、涂胶 | 永久放松 | - |
单个螺栓强度计算
| 类别 | 失效形式 | 计算准则 |
|---|---|---|
| 受拉螺栓 | 断裂 | 静力/疲劳 拉伸强度 |
| 受剪螺栓 | 压溃或剪断 | 挤压强度和剪切强度 |
下面只考虑受拉螺栓
只受到预紧力的紧螺纹连接
这种连接是靠结合面处的摩擦来传递横向载荷,为了避免相对滑移,因此必须有:
当然这个还受到应力的限制,因此有:
其中,螺纹连接不仅受预紧力拉力的作用,还有横向载荷扭矩的作用,因此需要考虑这个。根据第四强度理论对大量螺栓进行统计分析可以得到:复合应力的计算只需要将拉伸应力增大30%即可
这种螺纹在冲击、振动和交变应力作用下会非常不可靠,而且所需直径一般比较大。但是由于结构简单,装配方便,一直在使用。为避免上述缺点,可以使用各种减压键来承受横向载荷。
受预紧力和轴向工作载荷的紧螺纹连接
分三步走:力的计算、静载荷下强度计算、变载荷下强度计算
受力分析
由于被连接件的弹性形变的恢复,最后螺栓收到的总拉力 F0≠F’+F,而是:
然后经过公式的换算有:
为了防止出现间隙,应该保证:
$C_1/(C_1+C_2)$ 为螺栓的相对刚度,为了提高螺栓的承载能力,应该使这个值尽量小
静载荷下强度计算
变载荷下强度计算
螺栓组连接的设计
结构设计
- 连接结合面几何形状常设计成轴对称
- 螺栓布置应该受力合理
- 应该预留一定的扳手空间
- 分布在同一圆上的螺栓数目,应该取4,6,8等偶数,方便划线和分度
- 避免螺栓受到偏载(加凸台/沉头座)
受力分析
收到轴向载荷的螺栓组连接
- z:螺栓数量
收到横向载荷的螺栓组连接
受到扭转力矩 T 的螺栓组连接
化简得
受到翻转力矩的螺栓组连接
需要验证三个式子:最大工作压力、不压溃、不出现间隙
工作压力:
- $L_\max$ 受力最大的螺栓 到翻转轴的距离
- $F_\max$ 受力最大螺栓受到的工作载荷
- $M$ 翻转扭矩
不压溃:
不出现间隙:
轴的设计
轴的类型与型号
| 类型 | 说明 | 举例 |
|---|---|---|
| 转轴 | 承受扭矩和弯矩的轴 | 转速箱里面连着斜齿轮的轴 |
| 心轴 | 只承受弯矩的轴 | 起重机吊钩的轴 |
| 传动轴 | 只承受扭矩的轴 | 转速箱那个原动机引出的轴 |
一般轴用的材料有两大类:碳素钢、合金钢
碳素钢 45钢 用的最多。碳素钢价格低廉、对应力集中敏感性小
合金钢的力学性能和淬火性能比碳素钢要好,但对应力比较敏感,而且价格高
合金钢与碳素钢在常温下 弹性模量 差不多,因此,用合金钢并不能有效提高材料刚性
轴的设计过程
应力特点
- 弯曲应力:对称循环应力
- 扭转剪切应力:同转矩
设计准则
主要失效形式为:疲劳断裂
设计时一般进行 疲劳强度计算
对有刚度要求的轴(车床主轴)要进行 刚度计算 ,瞬时过载很大,则需要 按照最大载荷计算静强度 ,对高速轴还要进行 稳定振动分析
设计过程
1 | |
轴径的初步估计
按 扭转强度 估算:
化简得:
轴的结构设计
制造安装要求
便于拆卸、便于安装、便于制造
- 做成阶梯轴
- 应有倒角(方便安装零件)
- 需要磨削的部分应有砂轮越程槽
- 键应靠近装零件的端部(安装观察方便)
- 键的应该位于同一轴线上(良好的工艺性)
- 齿轮宽度应该大于轴径的长度(使齿轮压紧)
固定要求
轴向定位
轴肩连接、套筒固定(不宜太长)、双螺母固定、轴端挡圈(端部)、弹性挡圈、紧定螺钉(传递离校)
周向固定
键
受力、应力要求
- 合理布置轴上传动零件位置
- 合理设置轴上零件的结构(减小弯矩、改善配合)
- 减少应力集中
- 提高表面质量
- 定位轴与端盖之间的轴向距离不能太小
- 轴承外圈应该与壳体之间有5-8mm间隙
- 脂润滑必须有密封装置
轴的强度计算
应力校核法
- $\alpha$ 应力修正系数。
| 转矩不变 | 脉动循环 | 对称循环 |
|---|---|---|
| 0.3 | 0.6 | 1 |
安全系数法
疲劳强度
- $K_\sigma$ 有效应力集中系数
- $\beta$ 表面质量系数
- $\varepsilon$ 绝对尺寸
| 工作状态 | 应力类型 | 应力幅 | 平均应力 |
|---|---|---|---|
弯曲应力一般情况 |
对称循环 | $\sigma_a=M/W$ | $\sigma_m=0$ |
弯曲应力轴不转或载荷和轴一起转 |
脉动循环 | $\sigma_a=M/(2W)$ | $\sigma_m=M/(2W)$ |
扭转应力一般情况 |
脉动循环 | $\tau_a=T/(2W_T)$ | $\tau_m=T/(2W_T)$ |
扭转应力 轴频繁正反转 |
对称循环 | $\tau_a=T/W_T$ | $\tau_m=0$ |
其中:$W_T=2W$
静强度
联轴器与离合器
联轴器和离合器都是用来连接轴与轴的,用来传递运动和扭矩
| 名称 | 作用 | 特点 |
|---|---|---|
| 联轴器 | 主要用于轴与轴的连接,以传递运动和扭矩 | 停机才能连接或分离 |
| 离合器 | 在及其工作中可以随时使两轴分离或结合 | ①可以随时控制启动、停车②可以控制变速和换挡③过载安全保护 |
计算扭矩
- K 为工作系数
滑动轴承
失效形式主要是:轴瓦的胶合和磨损
按滑动轴承受载荷的方向,可以将滑动轴承分为:径向轴承、止推轴承
滑动轴承的结构形式
径向轴承
整体式轴承
结构简单、磨损后间隙过大、轴径只能从端部安装、拆卸
适用于小型轴
剖分式轴承
适用范围十分广泛、可以通过增加垫片调整间隙
剖分面的位置垂直于载荷,可以防止剪切
剖分式轴瓦下轴瓦承载,上轴瓦不承载,因此有沟开在上轴瓦非承载区
推力滑动轴承
只能承受轴向载荷
轴瓦的材料与结构
要求
- 良好的强度
- 良好的塑形、减磨性、耐磨性、耐腐蚀性
- 抗胶合能力强
- 良好的导热性
- 易于跑合、制造
常用材料
主要有三大类:金属材料、粉末冶金材料、金属材料
轴承合金
又叫做巴氏合金,是轴承最好的材料
- 锡基轴承合金
- 铅基轴承合金
优点:有良好抗胶合能力、的耐磨性、跑和性、塑形等
缺点:强度不高、价格昂贵
青铜
抗胶合能力强,仅次于轴承合金,强度较高
粉末冶金
可以制作称为含油轴承
有成本低、耐磨性好、强度高的优点
轴承结构
- 有沟应该开在非承载区
- 油沟长度小于轴承长度
非液体润滑轴承的计算
主要失效形式:胶合、磨损
对于这两种失效形式,目前还没有完善的设计计算方法。一般从限制轴承压强 p 和限制轴承压强与圆周速度的乘积 pv 进行计算,对于压强小的轴承,还应该验算其速度
在设计是一般知道 载荷、轴径、转速
验算轴承平均压强
保证润滑油不被过大的压力挤出、避免轴瓦的过度磨损
- B:轴承的工作宽度
- d:轴颈直径
验算轴承的 pv 值
限制功耗、避免温升
限制轴承速度
滑动轴承的润滑
液体摩擦轴承
- 重载、有冲击:高粘度
- 高速、轻载:低粘度
非液体摩擦轴承
当 K≤2 时,脂润滑;当 K>2 ,油润滑
动压滑动轴承的热平衡计算
液体动压润滑轴承
原理
假设
- 两板间流体做层流运动
- 两板间流体为牛顿流体,其粘度只与温度有关,忽略压力对其影响
- 与两板接触的流体层与板间无相对滑动
- 流体重力、惯性不考虑
- 由于间隙很小,压力沿纵向大小不变
- 平板无限长
公式
- $\eta$ 流体粘度
- $v$ 流体速度
- $h$ 任意处油膜厚度
- $h_0$ 当 $p=p_\max$ 时的油膜厚度
液体动压形成条件
- 流体有足够的速度
- 流体有足够的粘度
- 流体必须经过收敛间隙,而且收敛间隙越大,油膜的压力越大
液体动压轴承工程条件
承载能力
- $C_p$ 承载量系数,与长径比 B/d 有关
- $\psi=(R-r)/r$ 相对间隙。相对间隙大,轴的承载能力小。设计时根据载荷和速度选取($v\uparrow,F\downarrow\Rightarrow\psi\uparrow$)
- $B$ 工作宽度
最小油膜厚度
为了保证获得完全的液体摩擦,必须保证:轴承的最小油膜厚度大于轴颈和轴的表面粗糙度之和
油膜温度
根据上面热平衡计算式求
滚动轴承
主要失效形式为疲劳点蚀
重点在于滚动轴承的规格、类型、失效形式
滚动轴承的构造和特点
由外圈、内圈、滚动体、保持架组成
保持架将滚动体均匀的分布在内外圈之间,一般都需要
特点:
- 摩擦系数小、传动效率高
- 起动力矩小,启动灵活
- 润滑简单,耗油量小
- 标准件,易于更换
- 抗冲击能力差,很难做成剖分式
- 径向尺寸比滑动轴承大
滚动轴承的类型
轴承公称接触角 $\alpha$ :滚动体与套圈接触处的法线 与 轴承径向平面 之间的夹角
| 类型 | 公称接触角 | 举例 |
|---|---|---|
| 径向接触轴承 | $\alpha=0$ | 深沟球轴承、圆柱滚子轴承 |
| 向心角接触轴承 | $0<\alpha\leq\pi/4$ | 角接触球轴承 |
| 推力角接触轴承 | $\pi/4<\alpha<\pi/2$ | 推力角接触球轴承 |
| 轴向接触轴承 | $\alpha=\pi/2$ | 推力球轴承 |
常用滚动轴承的特性如图:
| 轴承名称及类型代号 | 转速 | 主要特性及应用 |
|---|---|---|
| 调心球轴承 1 | 中 | 主要从承受径向载荷,可同时承受双向轴向载荷;外圈滚道为球面,具有自动调心功能;适用于多支点轴、弯曲刚度小的轴 |
| 调心滚子轴承 2 | 低 | 径向承载能力比调心球轴承大,其余特点与上面相似 |
| 推力调心滚子轴承 2 | 低 | 可以承受很大的径向载荷和一定的轴向载荷,能够自动调心 |
| 圆锥滚子轴承 3 | 中 | 只能承受单方向轴向力、内外圈可以分离,轴承游隙可以在安装时调整 |
| 推力球轴承 5 | 低 | 套圈和滚动体可分离 |
| 深沟球轴承 6 | 高 | 主要承受径向力、可以承受极少量轴向力,极限转速高,价格便宜 |
| 角接触球轴承 7 | 较高 | 可取$\alpha=15,25,40$,公称接触角越大,轴向承载能力越大 |
| 圆柱滚子轴承 N | 较高 | 只能承受径向载荷 |
选择:
- 载荷大,有冲击 => 滚子轴承
- 转速高 => 球轴承
- 便宜 => 球轴承
滚动轴承的代号
滚动轴承由 前置代号、基本代号、后置代号 组成
基本代号
由 类型代号、尺寸系列代号、内径代号 组成
类型代号见上表格尺寸系列代号由 轴承的宽(高)系列代号(本质上是承载能力的不同) 和 直径代号组合而成。
| 说明 | 窄 0 | 正常 1 | 宽 2 |
|---|---|---|---|
| 轻 2 | 02 | 12 | 22 |
| 中 3 | 03 | 13 | 23 |
| 重 4 | 04 | 14 | 24 |
内径代号一般是用 直径/5 来表示,下面是一些特殊情况
| 00 | 01 | 02 | 03 | 用”/“隔开 |
|---|---|---|---|---|
| 10mm | 12mm | 15mm | 17mm | 本身 |
后置代号
内部结构代号
| C | AC | B | E |
|---|---|---|---|
| 角接触球轴承 $\alpha=15$ | 角接触球轴承 $\alpha=25$ | 角接触球轴承 $\alpha=40$ ;圆锥滚子轴承接触角加大 | 加强型 |
公差等级代号含有 P 的,常见的有 /P6、/P5、/P4、/P2
轴承装配代号常见的有 /DB、/DF、/DT
| /DB | /DF | /DT |
|---|---|---|
| 背对背(小口对小口) | 面对面(大口对大口) | 串联安装 |
例如:7210 C/P5/DF 表示这是一个角接触球轴承,基本尺寸代号为(02)属于窄轻系列,内径为50mm,该轴承公称接触角 $\alpha=15$ ,公差等级5级,属于面对面安装
失效形式
受到交变载荷(由于轴承的弹性变形引起的)
- 疲劳点蚀,最主要的失效形式
- 塑形变形
- 磨损
- 胶合
计算准则
计算准则主要是进行寿命计算,对低速轴承还可以进行 静强度计算,对高速轴承还可以验算 极限转速
寿命计算
寿命计算的本质还是强度计算
基本额定寿命
一批相同轴承,在相同条件下运转,90%轴承在疲劳点蚀前转过的转速
基本额定动载荷
轴承温度在100℃以下,基本额定寿命为10^6转时,轴承所能承受的最大载荷
方向:向心轴承 => 径向力;推力轴承 => 轴向力;角接触 => 径向分力
由实验可以推导出:
$P^\varepsilon L=$ 常数
- $P$:当量动载荷
- $\varepsilon$ :寿命系数,球轴承 $\varepsilon=3$,滚子轴承 $\varepsilon=10/3$
- $L$:寿命(以次数为单位)
引入基本额定动载荷,可以得到
化简得寿命
将次数转化为时间,并引入温度系数,对 C 值进行修正,得
- $L_h(h)$ 轴承寿命
- $C$ 基本额定动载荷
- $f_t$ 温度系数(温度越高,温度系数越低)
- $\varepsilon$ 寿命系数,球轴承 $\varepsilon=3$ ,滚子轴承 $\varepsilon=10/3$
- $n(r/\min)$ 转速
- $P(N)$ 当量动载荷
下面讨论 $P$ 的计算
- $X,Y$ 径向动载荷系数,轴向动载荷系数
- $f_P$ 冲击载荷系数
角接触轴承轴向力的判断
由内部派生轴向力与外部轴向力综合影响的叠加
内部轴向力:
方向
使内外圈脱离的方向,即由小口指向大口
大小
| 轴承类型 | 角接触球轴承C | 角接触球轴承AC | 角接触球轴承B | 圆锥滚子轴承 |
|---|---|---|---|---|
| $F_S$ | $0.5F_r$ | $0.7F_r$ | $1.1F_r$ | $F_r/(2Y)$ |
轴向力判断方法
- 判明轴上全部轴向力(包括外载荷 $F_A$ 和内部轴向力 $F_S$),合力指向,确定
压紧端和放松端 压紧端轴向力 = ∑所有轴向力(除自身内部轴向力外)放松端轴向力 = 自身轴向力
注意圆锥滚子轴承和角接触球轴承都只能承受单向载荷
静载荷计算
非重点
- $S_0$ :静载荷安全系数
对于向心轴承,有
取最大值
对于推力轴承
对于推力角接触球轴承
极限转速
非重点
- $f_1$ 载荷系数
- $f_2$ 载荷分布系数
- $n_\lim$ 在一定载荷和润滑条件下所允许的最大转速
滚动轴承的轴向固定
目的
- 控制轴相对于基座的轴向移动,抵抗轴向力
- 保证发热变形时有伸缩的可能
两端固定支撑
适用于普通工作温度下跨距小于 $l\leq300—500$ 的 短轴
此时,轴承盖与轴承之间,故意留了一个很小的间隙 $c=0.2-0.4mm$
轴的轴向力通过轴肩传递给轴承,轴承传递给端盖,最后端盖通过连接螺钉传递给机座
一端固定一端游动
适用于 轴较长或工作温度较高 的轴
固定端内圈固定在轴上,外圈固定在基座上,形成固定
移动端若为深沟球轴承,外圈与端盖间留有一定间隙,以此游动
移动端若为圆柱滚子轴承,可以进行双向固定,考滚子与套筒间的相对运动来游动
两端游动支撑
利用人字齿轮确定位置。在使用人字齿轮时,大齿轮被定死,小齿轮由于人字齿轮存在误差,必须要左右移动,此时就需要两端游动
人字齿轮,小齿轮两端游动,大齿轮两端固定
滚动轴承部件的调整与拆装
- 轴承游隙的调整
- 加减垫片
- 调整螺钉
- 传动件位置的调整(还是垫片)
其中 垫片1 是为了调整锥齿轮位置;垫片2 是为了调整轴承游隙。画图时要注意
轴承预紧
预先施加外力,消除游隙,提高刚度、旋转精度。
轴承的配合
- 标注:轴与内圈配合:只标轴;外圈与孔配合:只标孔
- 紧配合用于转速高、承载大、温度高的情况;松配合用于经常拆卸外圈静止的情况
轴承的装拆
- 加热
- 利用拆装工具
滚动轴承的润滑
$dn<(1.5-2)\times10^5$ 脂润滑
$dn>(1.5-2)\times10^5$ 油润滑
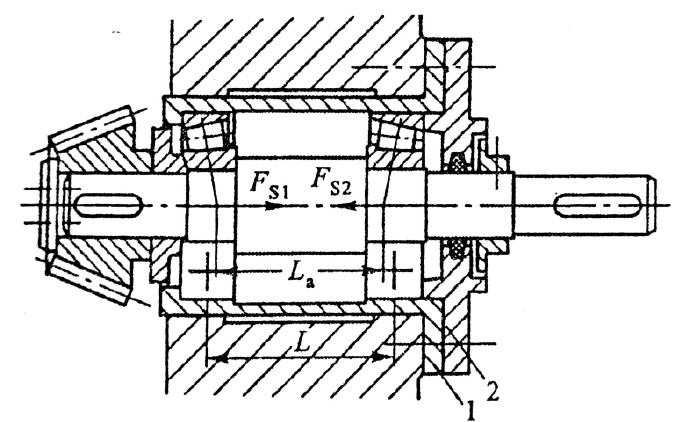
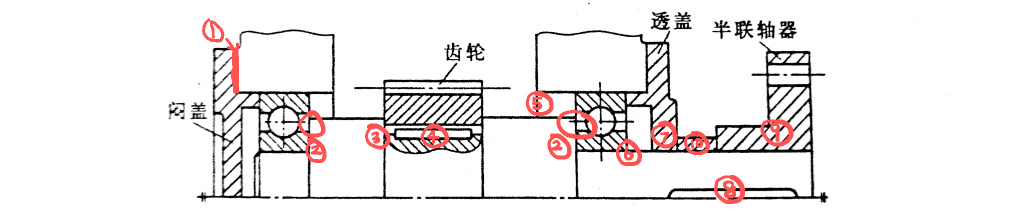
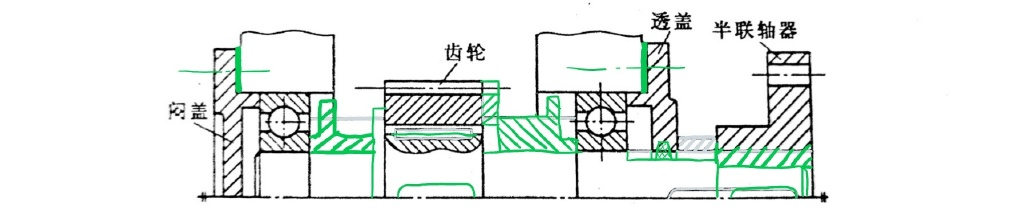
课本例题
如图为斜齿轮、轴、轴承、联轴器组合图。斜齿轮用油润滑,轴承用脂润滑,试改正错误。
| 序号 | 错误详情 |
|---|---|
| 1 | 端盖与机架之间应该有调整垫片,同时要有螺栓进行定位 |
| 2 | 轴肩高度超过轴承内圈,无法拆卸 |
| 3 | 轴肩高度过低,无法装配;应使用套筒进行轴向定位,此时轴肩宽度应该略小于齿轮宽度 |
| 4 | 键槽不在同一母线上,不方便加工 |
| 5 | 此处需要挡油板 |
| 6 | 轴承装配距离过长,应该设计成阶梯轴 |
| 7 | 此处应该考虑密封,同时,转动体与非转动体之间要有间隙 |
| 8 | 键槽过宽 |
| 9 | 轮毂宽度应该大于对应轴的宽度 |
| 10 | 转动体非转动体之间不能互相定位 |
Learning By Sharing,2018©Fu_Qingchen,Markdown,LaTeX