深度学习中的数学基础笔记

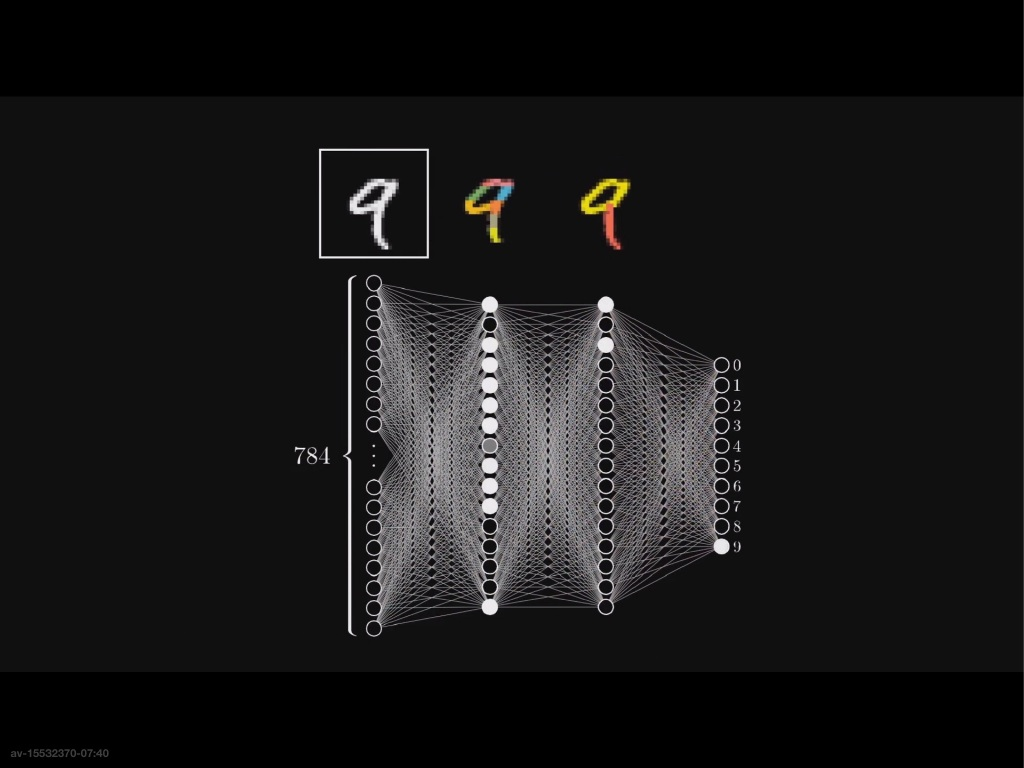
挺火的一个概念，选了一节公选课上，不过最后也就学了个皮毛。截图是来自 3Blue1Brown 数学频道，以文字识别为例

神经网络的架构

1. 神经元：神经元就相当于一个函数，输入以上一层为输入，输出给下一层。在文字识别中，一个神经元就是一个文字图像中一个像素的颜色深浅。这些深浅不一的像素（神经元）就组成了我们的文字。
2. 在神经网络中，神经元将自己的数据一层一层的传递，最后得到了最终的结果。例如文字识别中，第一层识别小的笔画，然后将自己的数据传递给下一层，然后再识别大的笔画，最终识别出来的文字

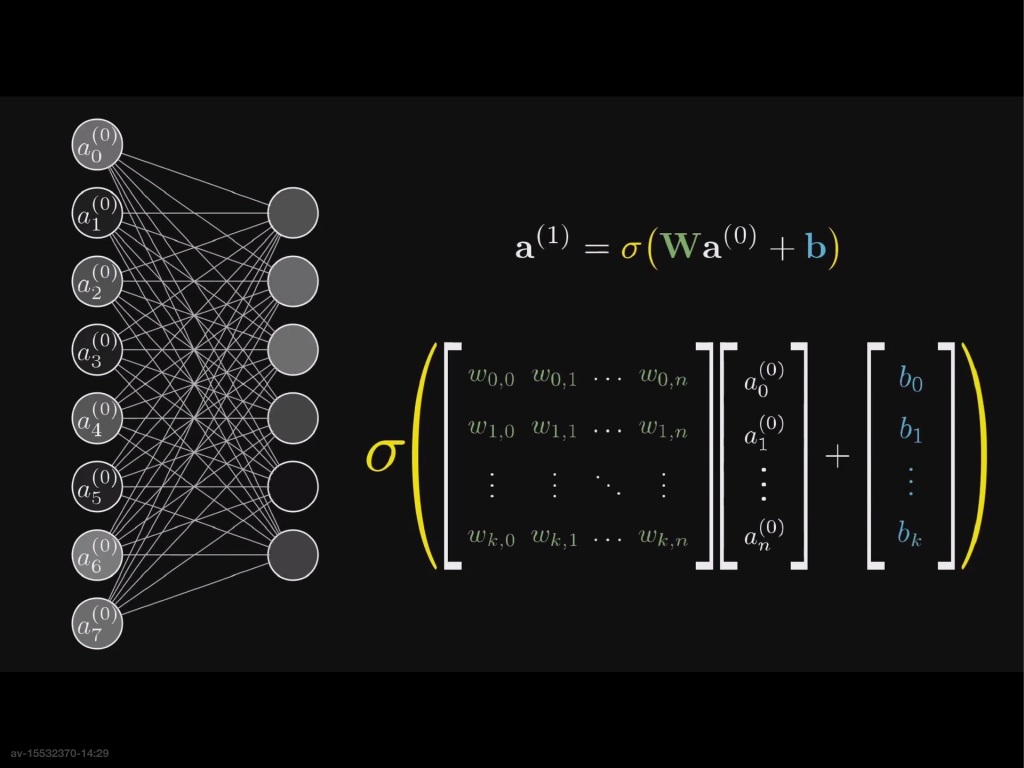
1. 识别的过程：以第二层的神经元为例，第一层的一个神经元要想识别小笔画，就必须要对第一层的每一个数据$a$，赋予一个权重$w$（表示第一层的那个神经元对这个地方的敏感程度）然后求和，得到这个神经元所代表的的数值

   $$w_1a_1+w_2a_2+...+w_na_n$$

   在实际情况中需要这个值在 0~1 之间，因此需要给它将这个数据减去加上一个函数（比如Sigmoid函数）

   $$\sigma(w_1a_1+w_2a_2+...+w_na_n)$$

   不过，$w_1a_1+w_2a_2+…+w_na_n$ 的出来可以是任何数，直接用上面的公式表示会出现过早激发的现象，因此需要减去一个偏置值$b$

   $$\sigma(w_1a_1+w_2a_2+...+w_na_n-b)$$

   这样的话就得到了第二层神经元的数据，以此类推，可以得到最终结果。

   用向量表示，可以得到下面的（$a^{(0)}$ 为第0层神经元的数值（激活值））

   $$a^{(1)}=\sigma(Wa^{(0)}+b)$$

梯度下降法

上面我们得到了那个可以计算激活值的递推方程，但是一开始的时候，上面所有的系数都是随机的，因此此时得到的结果误差会非常大。梯度下降算法能够使得这些系数得到的偏差最小。为了表示这个偏差，引出代价函数的概念，下面是一种常见的代价函数

$$Cost=\sum(\hat y^{(i)}-y^{(i)})^2$$

我们的目标就是使得这个函数的值最小。而沿着这个函数的负梯度方向走，这个函数的函数值就下降的越快，因此让这个函数变小的算法就出来了：

st=>start: 开始
op1=>operation: 计算梯度
op2=>operation: 按照梯度反方向走一小步下山
op3=>condition: 精度要求是否达到
e=>end: 结束

st->op1->op2->op3
op3(yes)->e
op3(no)->op1

相关的数学公式为

$$\vec{W} = \vec W-\bigtriangledown C(\vec W)$$

反向传播算法

反向传播算法的核心就是计算上面提到的梯度 $\bigtriangledown C$

先考虑两个神经元之间的传播。

记第一个神经元的所有参数上角标为$(L-1)$，下角标为$L$ .

因此有以下参数：

• $a^{(L-1)},a^{(L)}$ 两个神经元的激活值
• $w^{(L)}，b^{(L)}$ 从（L-1）层到（L）层的权重
• $y^{(L)}$ 想要达到的激活值

为了计算的方便，记 $z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}$，则有

$$C^{(L)}=(y^{(L)}-a^{(L)})^2\\ a^{(L)}=\sigma(z^{(L)})\\ z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}$$

由$a^{(L-1)}$到$a^{(L)}$ 的计算的过程是

w=>operation: w(L)，a(L-1)，b(L)
z=>operation: z(L)
a2=>operation: a(L)
C=>operation: C(L)
w->z->a2->C

而要求的是

$$\frac{\partial C^{(L)}}{\partial w^{(L)}}=\frac{\partial C^{(L)}}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial w^{(L)}}$$

根据上面的方程可以得到

$$\frac{\partial C^{(L)}}{\partial a^{(L)}}=2(a^{(L)}-y^{(L)})\\ \frac{\partial a^{(L)}}{\partial z^{(L)}}=\sigma'(z^{(L)})\\ \frac{\partial z^{(L)}}{\partial w^{(L)}}=a^{(L-1)}\\ \frac{\partial C^{(L)}}{\partial w^{(L)}}=\frac{\partial C^{(L)}}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial w^{(L)}}=2(a^{(L)}-y^{(L)})\sigma'(z^{(L)})a^{(L-1)}$$

同理

$$\frac{\partial C^{(L)}}{\partial w^{(L)}}=2(a^{(L)}-y^{(L)})\sigma'(z^{(L)})a^{(L-1)}\\ \frac{\partial C^{(L)}}{\partial a^{(L-1)}}=2(a^{(L)}-y^{(L)})\sigma'(z^{(L)})w^{(L)}\\ \frac{\partial C^{(L)}}{\partial b^{(L)}}=2(a^{(L)}-y^{(L)})\sigma'(z^{(L)})$$

将这个简单的两个神经元之间的传播扩展到一般情况

$$C^{(L)}=\sum\limits_{i}(y^{(L)}_i-a^{(L)}_i)^2\\ a_i^{(L)}=\sigma(z_i^{(L)})\\ z_i^{(L)}=\sum\limits_{j}w_{ij}^{(L)}a_j^{(L-1)}+b_i^{(L)}$$

其中，i是上层的第i个神经元；j为下层的第j个神经元

$$\frac{\partial C^{(L)}}{\partial w_{ij}^{(L)}}=\frac{\partial C^{(L)}}{\partial a_i^{(L)}}\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}\frac{\partial z_i^{(L)}}{\partial w_{ij}^{(L)}}=2(a_i^{(L)}-y_i^{(L)})\sigma'(z_i^{(L)})a_j^{(L-1)}$$

实际举例

构建一个四层的BP人工神经网络，不少于16个神经元结点，自定义一个样本，模拟计算一次完整的样本训练过程，整个过程必须包括各个神经元结点的输入值、输出值以及反馈过程中对权向量的修改情况。

构建的网络

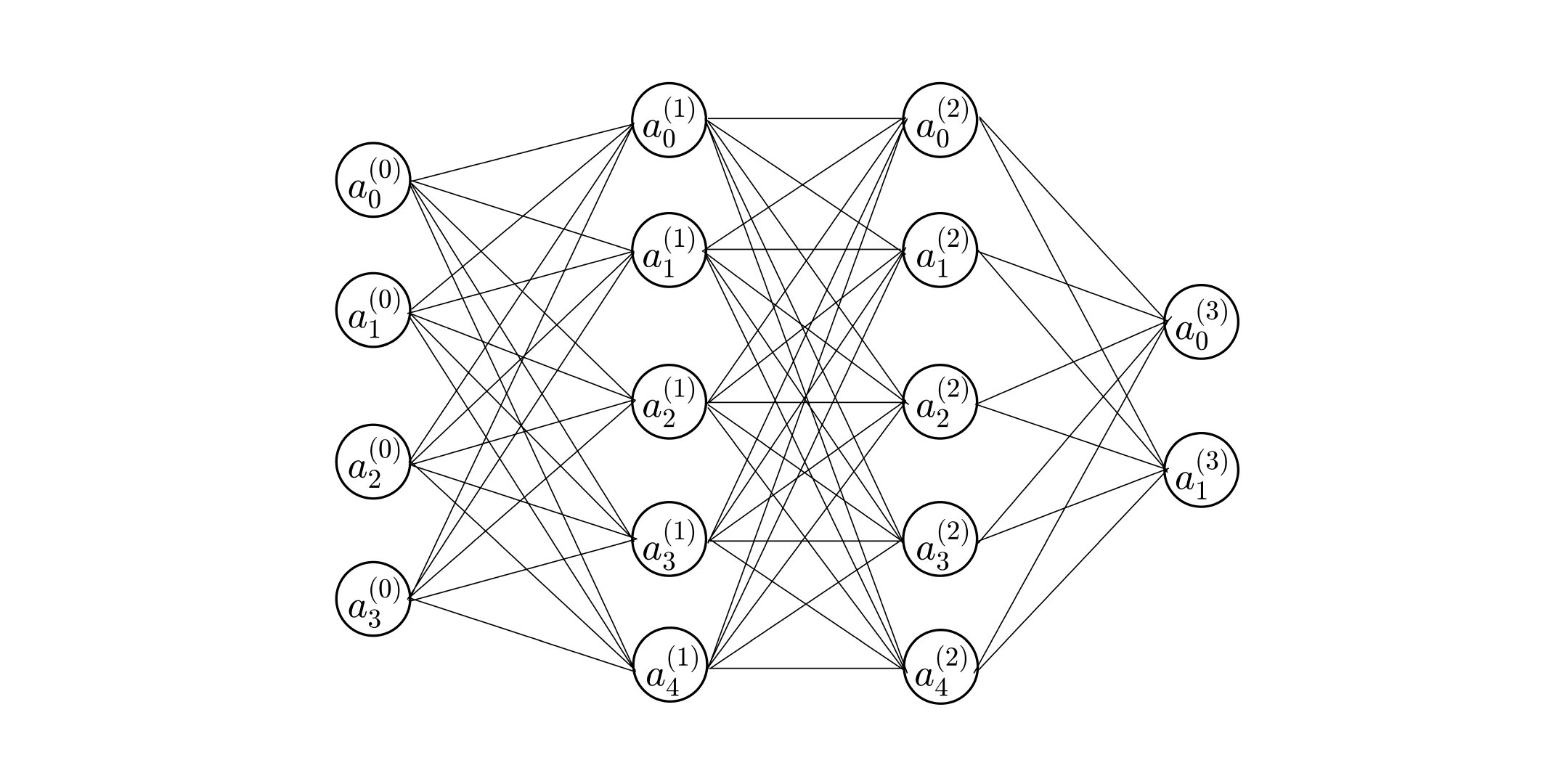
其中：

• 输入层 $a^{(0)}=\left[4\ 3\ 2\ 1 \right]^T$
• 权重 $w^{(1)}=\left[
  \begin{matrix}
  0.01 & 0.06 & 0.11 & 0.16\\
  0.02 & 0.07 & 0.12 & 0.17\\
  0.03 & 0.08 & 0.13 & 0.18\\
  0.04 & 0.09 & 0.14 & 0.19\\
  0.05 & 0.10 & 0.15 & 0.20\\
  \end{matrix}
  \right],w^{(2)}=\left[
  \begin{matrix}0.21 & 0.22 & 0.23 &0.24 & 0.25\\
  0.16 & 0.17 & 0.18 &0.19 & 0.20\\
  0.11 & 0.12 & 0.13 &0.14 & 0.15\\
  0.06 & 0.07 & 0.08 & 0.09 & 0.10\\
  0.01 & 0.02 & 0.03 & 0.04 & 0.05\\\end{matrix}
  \right],w^{(3)}=\left[
  \begin{matrix}
  0.16 & 0.21 \\0.17 & 0.22 \\ 0.18 &0.23\\0.19 & 0.24\\0.20 & 0.25\\
  \end{matrix}
  \right]^T$
• 期望输出层 $y^{(3)}=[0.10\ 0.24]^T$
• 每个节点没有偏置
• 节点激活函数 $\sigma(x)=1/{(1+e^{-x})}$，导数$\sigma’(x)=\sigma(x)(1-\sigma(x))$

符号说明

• $a_i^{(L)}$：第 (L) 层节点的第 i 个元素的 输出值
• $z_i^{(L)}$：第 (L) 层节点的第 i 个元素的 输入值
• $w_{ij}^{(L)}$：第 (L-1) 层 的第 i 个节点 到 第 (L) 层 的第 j 个节点的 权重

正向传播

0层→1层

第一层输入值为：

$$z^{(1)}=\left[ \begin{matrix} z_0^{(1)} \\ z_1^{(1)} \\ z_2^{(1)} \\ z_3^{(1)} \\ \end{matrix} \right]=w^{(1)}a^{(0)}=\left[ \begin{matrix} w_{00}^{(1)} & w_{01}^{(1)} & w_{02}^{(1)} & w_{03}^{(1)}\\ w_{10}^{(1)} & w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)}\\ w_{20}^{(1)} & w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)}\\ w_{30}^{(1)} & w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)}\\ w_{40}^{(1)} & w_{41}^{(1)} & w_{42}^{(1)} & w_{43}^{(1)}\\ \end{matrix} \right]·\left[ \begin{matrix} a_0^{(0)} \\ a_1^{(0)} \\ a_2^{(0)} \\ a_3^{(0)} \\ \end{matrix} \right]\\=\left[ \begin{matrix} 0.01 & 0.06 & 0.11 & 0.16\\ 0.02 & 0.07 & 0.12 & 0.17\\ 0.03 & 0.08 & 0.13 & 0.18\\ 0.04 & 0.09 & 0.14 & 0.19\\ 0.05 & 0.10 & 0.15 & 0.20\\ \end{matrix} \right]·\left[ \begin{matrix} 4\\ 3\\ 2\\ 1\\ \end{matrix} \right]=\left[ \begin{matrix} 0.6\\ 0.7\\ 0.8\\ 0.9\\ 1.0\\ \end{matrix} \right]$$

第一层输出值为：

$$a^{(1)}=\left[ \begin{matrix} a_0^{(1)} \\ a_1^{(1)} \\ a_2^{(1)} \\ a_3^{(1)} \\ \end{matrix} \right]=\sigma\left(z^{(1)}\right)=\sigma\left(\left[ \begin{matrix} 6\\ 7\\ 8\\ 9\\ 10\\ \end{matrix} \right]\right)=\left[ \begin{matrix} 0.6457\\ 0.6682\\ 0.6900\\ 0.7109\\ 0.7311\\ \end{matrix} \right]$$

1层→2层

第二层输入值为：

$$z^{(2)}=\left[ \begin{matrix} z_0^{(2)} \\ z_1^{(2)} \\ z_2^{(2)} \\ z_3^{(2)} \\ z_4^{(2)} \\ \end{matrix} \right]=w^{(2)}a^{(1)}=\left[ \begin{matrix} w_{00}^{(2)} & w_{01}^{(2)} & w_{02}^{(2)} & w_{03}^{(2)} & w_{04}^{(2)}\\ w_{10}^{(2)} & w_{11}^{(2)} & w_{12}^{(2)} & w_{13}^{(2)} & w_{04}^{(2)}\\ w_{20}^{(2)} & w_{21}^{(2)} & w_{22}^{(2)} & w_{23}^{(2)} & w_{04}^{(2)}\\ w_{30}^{(2)} & w_{31}^{(2)} & w_{32}^{(2)} & w_{33}^{(2)} & w_{04}^{(2)}\\ w_{40}^{(2)} & w_{41}^{(2)} & w_{42}^{(2)} & w_{43}^{(2)} & w_{04}^{(2)}\\ \end{matrix} \right]·\left[ \begin{matrix} a_0^{(1)} \\ a_1^{(1)} \\ a_2^{(1)} \\ a_3^{(1)} \\ a_4^{(1)} \\ \end{matrix} \right]\\=\left[ \begin{matrix} 0.21 & 0.22 & 0.23 &0.24 & 0.25\\ 0.16 & 0.17 & 0.18 &0.19 & 0.20\\ 0.11 & 0.12 & 0.13 &0.14 & 0.15\\ 0.06 & 0.07 & 0.08 & 0.09 & 0.10\\ 0.01 & 0.02 & 0.03 & 0.04 & 0.05\\ \end{matrix} \right]·\left[ \begin{matrix} 0.6457\\ 0.6682\\ 0.6900\\ 0.7109\\ 0.7311\\ \end{matrix} \right]=\left[ \begin{matrix} 0.7947\\ 0.6224\\ 0.4501\\ 0.2778\\ 0.1055\\ \end{matrix} \right]$$

第二层输出值为：

$$a^{(2)}=\left[ \begin{matrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \\ \end{matrix} \right]=\sigma\left(z^{(2)}\right)=\sigma\left(\left[ \begin{matrix} 0.7947\\ 0.6224\\ 0.4501\\ 0.2778\\ 0.1055\\ \end{matrix} \right]\right)=\left[ \begin{matrix} 0.6888\\ 0.6508\\ 0.6107\\ 0.5690\\ 0.5264\\ \end{matrix} \right]$$

2层→3层

第三层输入值为：

$$z^{(3)}=\left[ \begin{matrix} z_0^{(3)} \\ z_1^{(3)} \\ \end{matrix} \right]=w^{(3)}a^{(2)}=\left[ \begin{matrix} w_{00}^{(3)} & w_{01}^{(3)} & w_{02}^{(3)} & w_{03}^{(3)} & w_{04}^{(3)}\\ w_{10}^{(3)} & w_{11}^{(3)} & w_{12}^{(3)} & w_{13}^{(3)} & w_{04}^{(3)}\\ \end{matrix} \right]·\left[ \begin{matrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \\ a_4^{(2)} \\ \end{matrix} \right]\\=\left[ \begin{matrix} 0.16 & 0.17 & 0.18 & 0.19 & 0.20\\ 0.21 & 0.22 & 0.23 & 0.24 & 0.25\\ \end{matrix} \right]·\left[ \begin{matrix} 0.6888\\ 0.6508\\ 0.6107\\ 0.5690\\ 0.5264\\ \end{matrix} \right]=\left[ \begin{matrix} 0.5441\\ 0.6964\\ \end{matrix} \right]$$

第三层输出值为：

$$a^{(3)}=\left[ \begin{matrix} a_0^{(3)} \\ a_1^{(3)} \\ \end{matrix} \right]=\sigma\left(z^{(3)}\right)=\sigma\left(\left[ \begin{matrix} 0.7947\\ 0.6224\\ \end{matrix} \right]\right)=\left[ \begin{matrix} 0.6328\\ 0.6674\\ \end{matrix} \right]$$

误差

$$C^{(3)}=\sum\limits_i\frac12(y_i^{(3)}-a_i^{(3)})^2\\=\frac 12(0.6328-0.10)^2+\frac 12(0.6674-0.24)^2=0.2332$$

反向传播

3层→2层

有以下数学关系：

$$C^{(3)}=\frac12(y^{(3)}-a^{(3)})^2\\ a^{(3)}=\sigma(z^{(3)})\\ z^{(3)}=w^{(3)}a^{(2)}$$

因此 权重梯度

$$\bigtriangledown w_{ij}^{(3)}=\frac{\partial C^{(3)}}{\partial w_{ij}^{(3)}}=\frac{\partial C^{(3)}}{\partial a_i^{(3)}}\frac{\partial a_i^{(3)}}{\partial z_i^{(3)}}\frac{\partial z_i^{(3)}}{\partial w_{ij}^{(3)}}=(a_i^{(3)}-y_i^{(3)})\sigma(z_i^{(3)})[1-\sigma(z_i^{(3)})]a_j^{(2)}\\ \bigtriangledown w^{(3)}=\left[ \begin{matrix} 0.0853 & 0.0806 & 0.0756 & 0.0704 & 0.0652\\ 0.0654 & 0.0617 & 0.0579 & 0.0540 & 0.0499\\ \end{matrix} \right]$$

修正后权重：

$$w^{(3)'}=w^{(3)}-\bigtriangledown w^{(3)}=\left[ \begin{matrix} 0.0747 & 0.0894 & 0.1044 & 0.1196 & 0.1348\\ 0.1446 & 0.1583 & 0.1721 & 0.1860 & 0.2001\\ \end{matrix} \right]$$

2层→1层

有以下数学关系：

$$C^{(3)}=\frac12(y^{(3)}-a^{(3)})^2\\ a^{(3)}=\sigma(z^{(3)})\\ z^{(3)}=w^{(3)}a^{(2)}\\ a^{(2)}=\sigma(z^{(2)})\\ z^{(2)}=w^{(2)}a^{(1)}\\$$

因此 权重梯度

$$\bigtriangledown w_{ij}^{(2)} =\frac{\partial C^{(3)}}{\partial w_{ij}^{(2)}} =\frac{\partial C^{(3)}}{\partial a_i^{(2)}}\frac{\partial a_i^{(2)}}{\partial z_{i}^{(2)}}\frac{\partial z_i^{(2)}}{\partial w_{ij}^{(2)}} =\frac{\partial C^{(3)}}{\partial a_i^{(2)}}\sigma(z_i^{(2)})[1-\sigma(z_i^{(2)})]a_j^{(1)}\\ \bigtriangledown w^{(2)}=\left[ \begin{matrix} 0.0032 & 0.0033 & 0.0034 & 0.0035 & 0.0036\\ 0.0038 & 0.0040 & 0.0041 & 0.0042 & 0.0043\\ 0.0045 & 0.0046 & 0.0048 & 0.0049 & 0.0051\\ 0.0051 & 0.0053 & 0.0055 & 0.0057 & 0.0058\\ 0.0057 & 0.0059 & 0.0061 & 0.0063 & 0.0065\\ \end{matrix} \right]$$

其中

$$\frac{\partial C^{(3)}}{\partial a_i^{(2)}} =\sum\limits_i\frac{\partial C^{(3)}}{\partial a_i^{(3)}}\frac{\partial a_i^{(3)}}{\partial z_i^{(3)}}\frac{\partial z_i^{(3)}}{\partial a_{j}^{(2)}} =\sum\limits_i\frac{\partial C^{(3)}}{\partial a_i^{(3)}}a_i^{(3)}(1-a_i^{(3)})w_{ij}^{(3)'}\\$$

修正后权重：

$$w^{(2)'}=w^{(2)}-\bigtriangledown w^{(3)}=\left[ \begin{matrix} 0.2068 & 0.2167 & 0.2266 & 0.2365 & 0.2464\\ 0.1562 & 0.1660 & 0.1759 & 0.1858 & 0.1957\\ 0.1055 & 0.1154 & 0.1252 & 0.1351 & 0.1449\\ 0.0549 & 0.0647 & 0.0745 & 0.0843 & 0.0942\\ 0.0043 & 0.0141 & 0.0239 & 0.0337 & 0.0435\\ \end{matrix} \right]$$

1层→0层

有以下数学关系：

$$C^{(3)}=\frac12(y^{(3)}-a^{(3)})^2\\ a^{(3)}=\sigma(z^{(3)})\\ z^{(3)}=w^{(3)}a^{(2)}\\ a^{(2)}=\sigma(z^{(2)})\\ z^{(2)}=w^{(2)}a^{(1)}\\ a^{(1)}=\sigma(z^{(1)})\\ z^{(1)}=w^{(1)}a^{(0)}\\$$

因此 权重梯度

$$\bigtriangledown w_{ij}^{(1)} =\frac{\partial C^{(3)}}{\partial w_{ij}^{(1)}} =\frac{\partial C^{(3)}}{\partial a_i^{(1)}}\frac{\partial a_i^{(1)}}{\partial z_{i}^{(1)}}\frac{\partial z_i^{(2)}}{\partial w_{ij}^{(1)}} =\frac{\partial C^{(3)}}{\partial a_i^{(1)}}\sigma(z_i^{(1)})[1-\sigma(z_i^{(1)})]a_j^{(0)}\\ \bigtriangledown w^{(1)}=\left[ \begin{matrix} 0.0029 & 0.0022 & 0.0014 & 0.0007\\ 0.0031 & 0.0023 & 0.0015 & 0.0008\\ 0.0033 & 0.0025 & 0.0016 & 0.0008\\ 0.0034 & 0.0026 & 0.0017 & 0.0009\\ 0.0036 & 0.0027 & 0.0018 & 0.0009\\ \end{matrix} \right]$$

其中

$$\frac{\partial C^{(3)}}{\partial a_i^{(1)}} =\sum\limits_i\frac{\partial C^{(3)}}{\partial a_i^{(2)}}\frac{\partial a_i^{(2)}}{\partial z_i^{(3)}}\frac{\partial z_i^{(2)}}{\partial a_{j}^{(2)}} =\sum\limits_i\frac{\partial C^{(3)}}{\partial a_i^{(2)}}a_i^{(2)}(1-a_i^{(2)})w_{ij}^{(2)}\\$$

修正后权重：

$$w^{(1)'}=w^{(1)}-\bigtriangledown w^{(3)}=\left[ \begin{matrix} 0.0071 & 0.0578 & 0.1086 & 0.1593\\ 0.0169 & 0.0677 & 0.1185 & 0.1692\\ 0.0267 & 0.0775 & 0.1284 & 0.1792\\ 0.0366 & 0.0874 & 0.1383 & 0.1891\\ 0.0464 & 0.0973 & 0.1482 & 0.1991\\ \end{matrix} \right]$$

一次完整的样本训练过程就结束了

训练后误差

$$C^{(3)'}=\sum\limits_i\frac12(y_i^{(3)}-a_i^{(3)})^2\\=\frac 12(0.5769-0.10)^2+\frac 12(0.6259-0.24)^2=0.1882<0.2332=C^{(3)}$$

计算过程

Matlab代码，比较低级，算是半个手工计算。。。

Y = [0.10 0.24]';
W10 = [0.01:0.05:0.16;...
           0.02:0.05:0.17;...
           0.03:0.05:0.18;...
           0.04:0.05:0.19;...
           0.05:0.05:0.20];
A0 = [4 3 2 1]';
W20 = [0.21:0.01:0.25;...
           0.16:0.01:0.20;...
           0.11:0.01:0.15;...
           0.06:0.01:0.10;...
           0.01:0.01:0.05];
W30 =  [0.16:0.01:0.20;...
           0.21:0.01:0.25];
Z1 = W10*A0;
A1 = 1./(1.+exp(-Z1));
Z2 = W20*A1;
A2 = 1./(1.+exp(-Z2));
Z3 = W30*A2;
A3 = 1./(1.+exp(-Z3));
C = 0.5.*(Y - A3).*(Y - A3);
DW3 = (A3-Y).*(A3).*(1-A3)*A2';
W3 = W30 - DW3;
DA3 = A3-Y;
DA2 = (DA3.*A3.*(1-A3))'*W3;
DA2 = DA2';
DW2 = DA2.*A2.*(1-A2)*A1';
W2 = W20 - DW2;
DA1 = (DA2.*A2.*(1-A2))'*W2;
DA1 = DA1';
DW1 = DA1.*A1.*(1-A1)*A0';
W1 = W10 - DW1;

Z11 = W1*A0;
A11 = 1./(1.+exp(-Z11));
Z21 = W2*A11;
A21 = 1./(1.+exp(-Z21));
Z31 = W3*A21;
A31 = 1./(1.+exp(-Z31));
C1 = 0.5.*(Y - A31).*(Y - A31);

---

2018-10-21