理论力学回顾

最近搞毕业设计遇到了一些理论力学的问题，发现自己忘记的好快，所以来回顾一下。理论力学是各种力学的基础，讨论物体不失效，不变形情况下运动和力的关系

回顾

理论力学主要分为三大部分：

• 静力学：讨论静止状态下物体的受力，主要包括力的平衡，力系的简化。
• 运动学：讨论物体的运动状态，主要包括运动的描述，复合运动速度和加速度的求解。
• 动力学：讨论力和物体的关系。主要解决给定力求运动轨迹、速度。动力学求解方法有很多种，任意一种即可。

静力学

静力学内容比较少，也比较简单，其主要思想是分而治之。这一块的核心就是画受力分析图，然后根据受力分析图求解约束力。其中要注意的地方就是力和力偶的概念，还有他们的相互转化。其主要内容包括：

• 约束类型和约束力的数量和方向
• 受力分析图
• 力对点的力矩：$M_O(\vec{F})=\vec r\times \vec F$；力对轴的矩：$M_z(\vec{F})=[M_O(\vec F)]_z$
• 力的平移$F’\rightarrow F+M$；力偶的平移 $M\rightarrow M$
• 平面任意力系的平衡条件 $\vec F=0,M=0$
• 超静定问题的求解
• 摩擦角和自锁

运动学

运动学稍微多一点，但是同样比较简单，就是公式变多了。这一块的核心是选择动点动系画运动图，然后根据对应的公式进行求解。要注意点的绝对运动、相对运动、牵连运动的概念，然后有个科氏加速度。这一块的知识在机械原理中会在此用到。其主要内容是：

• 点的运动的表示

• 点的绝对运动（动点对定系）、相对运动（动点对动系）、牵连运动（动系对静系），并且有以下关系：

  • 速度：$\vec{v_a} = \vec{v_e} + \vec{v_r}$

  • 加速度（牵连运动是平动）：$\vec{a_a} = \vec{a_e} + \vec{a_r},a_r^n=v_r^2/R=\omega^2R$

  • 加速度（牵连运动是转动）：$\vec{a_a} = \vec{a_e} + \vec{a_r} + \vec{a_C},a_r^n=v_r^2/R=\omega^2R,\vec{a_C}=2\vec{\omega}\times\vec{v_r}$

• 刚体平面运动：

  • 速度：合成法（ $\vec{v_B} = \vec{v_A} + \vec{v_{BA}}$ ）、速度投影法（ $(\vec{v_A})_{AB}=(\vec{v_B})_{AB}$ ）、瞬心法
  • 加速度：合成法（ $\vec{a_B} = \vec{a_A} + \vec{a_{BA}},\vec{a_{BA}}=\vec{a_{BA}^n}+\vec{a_{BA}^t}$ ）

动力学

这一块内容很多很杂，求解方法也有很多。主要有两派，一派是以牛顿为主导的经典力学解法，在笛卡尔坐标系下用动量动量矩动能定理求解，另一派是以拉格朗日为主导的分析力学的解法，在广义坐标系下用拉格朗日方程求解。其中，分析力学以经典力学中的达朗贝尔原理和虚位移原理作为基础，主要研究功能关系，不需要复杂的运动学求解。

在这个里面最重要的思想是守恒，还有达朗贝尔原理、虚功原理和广义坐标系。这一块也是理论力学的核心，同时，这一块的知识在材料力学中会使用到。

经典力学主要内容如下：

• 质心运动定理（牛二） $m\vec {a_C}=\sum \vec{F_i^{(e)}}, J_C\alpha=\sum M_C(\vec{F_i^{(e)}})$
• 质点系动量定理 $d(\sum m\vec v)/dt=\sum \vec {F^{(e)}_i}$
• 质点系动量矩定理 $d[M_O(m\vec{v_C})+J_C\omega]/dt=\sum M_O(\vec{F_i^{(e)}})$
• 质点系动能定理 $T_2-T_1 = \sum W$
• 达朗贝尔原理（动静法）：惯性力代替加速度 $\sum\vec{F_i^{(e)}} + \sum\vec{F_I}=0,\sum M_O{(\vec{F_i^{(e)}})}+\sum M_O(\vec{F_I})=0,\vec{F_{IR}}=-m\vec {a_C},M_{IC}=-J_C\alpha$
• 虚位移原理：设定虚位移，研究虚位移之间的关系，所有主动力虚功为零$\sum \vec{F_i}·\delta\vec{r_i}=0$

分析力学主要内容如下：

• N维广义坐标下的坐标矢量 $\delta \vec{r_i}=\sum\limits_{k=1}^N(\partial\vec{r_i}/\partial q_k)\delta{q_k}$

• 广义坐标下的平衡条件：广义力为零 $Q_k=\sum\limits_{i=1}^n(F_{ix}\frac{\partial x_i}{\partial q_k}+F_{iy}\frac{\partial y_i}{\partial q_k}+F_{iz}\frac{\partial z_i}{\partial q_k})=0$

  确定广义坐标->写出质点在广义坐标下的表达式->表达式对广义坐标求导->求解广义力->广义力为0求解未知量

• 对保守系统（无外力的系统），质点系的势能对于每一个广 义坐标的偏导数分别等于零 $Q_k=-(\partial V/\partial q_k)=0$

• 动力学普遍方程：广义力与广义惯性力所作的虚功和为零 $\sum\limits_{i=1}^N(Q_k-\sum\limits_{k=1}^nm\ddot r·\frac{\partial r_i}{\partial q_k})\delta q_k=0$

• 拉格朗日方程

$$\frac{d}{dt}(\frac{\partial T}{\partial \dot {q_k}})-\frac{\partial T}{\partial {q_k}}-Q_k=0$$

小练习

import sympy as sym
sym.init_printing(use_latex="mathjax")

这个题目的来源是模拟 https://www.bilibili.com/video/BV17A411h7wJ 这个视频 10:33 的内容，通过这个巩固一下自己的理论力学和编程能力。

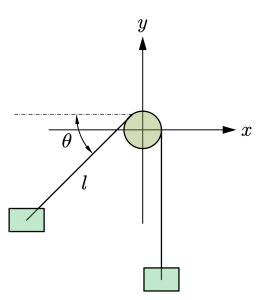
已知两个物体通过一根绳子挂在一根柱子上，其中有一个物体有动能，该物体运动至最高处的状态如图所示，忽略摩擦以及柱子的直径，求其运动方程

取如图所示$m,M$为物体质量，$l,\theta$为有动能的物体到柱子的长度和绳子的角度，绳子总长S，易得两个物体的坐标可以表示为

$$p_m=\left[ \begin{array}{c}-l\cos \theta\\-l\sin \theta\\\end{array} \right] ,p_M=\left[ \begin{array}{c}0\\l-L\\\end{array} \right]$$

对时间求导，可以得到他们的速度为

$$\dot{p}_m=\left[ \begin{array}{c} -\dot{l}\cos \theta +l\dot{\theta}\sin \theta\\ -\dot{l}\sin \theta -l\dot{\theta}\cos \theta\\ \end{array} \right] ,\dot{p}_M=\left[ \begin{array}{c} 0\\ \dot{l}\\ \end{array} \right]$$

l, theta, dl, dtheta, S = sym.symbols(r'l, theta, \dot{l}, \dot{\theta}, S')
pm, pM = sym.Matrix([-l*sym.cos(theta), -l*sym.sin(theta)]), sym.Matrix([0, l-S])
dpm, dpM = sym.Matrix([-dl*sym.cos(theta) + l*dtheta*sym.sin(theta), -dl*sym.sin(theta)-l*dtheta*sym.cos(theta)]), sym.Matrix([0, dl])
pm, pM, dpm, dpM

$$\left ( \left[\begin{matrix}- l \cos{\left (\theta \right )}\\- l \sin{\left (\theta \right )}\end{matrix}\right], \quad \left[\begin{matrix}0\\- S + l\end{matrix}\right], \quad \left[\begin{matrix}\dot{\theta} l \sin{\left (\theta \right )} - \dot{l} \cos{\left (\theta \right )}\\- \dot{\theta} l \cos{\left (\theta \right )} - \dot{l} \sin{\left (\theta \right )}\end{matrix}\right], \quad \left[\begin{matrix}0\\\dot{l}\end{matrix}\right]\right )$$

求解其动能和势能为

m, M , g= sym.symbols(r"m, M, g")
T = (1/2*m*dpm.T*dpm + 1/2*M*dpM.T*dpM)[0]
V = m*g*pm[1] + M*g*pM[1]
T, V

$$\left ( 0.5 M \dot{l}^{2} + 0.5 m \left(\dot{\theta} l \sin{\left (\theta \right )} - \dot{l} \cos{\left (\theta \right )}\right)^{2} + 0.5 m \left(- \dot{\theta} l \cos{\left (\theta \right )} - \dot{l} \sin{\left (\theta \right )}\right)^{2}, \quad M g \left(- S + l\right) - g l m \sin{\left (\theta \right )}\right )$$

L = T - V为

L = T - V
L

$$0.5 M \dot{l}^{2} - M g \left(- S + l\right) + g l m \sin{\left (\theta \right )} + 0.5 m \left(\dot{\theta} l \sin{\left (\theta \right )} - \dot{l} \cos{\left (\theta \right )}\right)^{2} + 0.5 m \left(- \dot{\theta} l \cos{\left (\theta \right )} - \dot{l} \sin{\left (\theta \right )}\right)^{2}$$

由拉格朗日方程得

$$\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{l}} \right) -\frac{\partial L}{\partial l}=0\\ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta}} \right) -\frac{\partial L}{\partial \theta}=0$$

func_temp = sym.Matrix([[sym.diff(L, dl), sym.diff(L, l)], 
            [sym.diff(L, dtheta), sym.diff(L,  theta)]])
sym.simplify(func_temp)

$$\left[\begin{matrix}1.0 \dot{l} \left(M + m\right) & - 1.0 M g + 1.0 \dot{\theta}^{2} l m + 1.0 g m \sin{\left (\theta \right )}\\1.0 \dot{\theta} l^{2} m & g l m \cos{\left (\theta \right )}\end{matrix}\right]$$

ddl, ddtheta = sym.symbols(r"\ddot{l}, \ddot{\theta}")
dLddl = ddl*(M + m)
dLddtheta = ddtheta*l**2*m + 2*dtheta*l*m*dl
sym.simplify(sym.Matrix([dLddl-sym.diff(L, l), dLddtheta-sym.diff(L,  theta)]))

$$\left[\begin{matrix}1.0 M \ddot{l} + 1.0 M g + 1.0 \ddot{l} m - 1.0 \dot{\theta}^{2} l m - 1.0 g m \sin{\left (\theta \right )}\\l m \left(\ddot{\theta} l + 2 \dot{\theta} \dot{l} - g \cos{\left (\theta \right )}\right)\end{matrix}\right]$$

整理得到微分方程

$$\left( m+M \right) \ddot{l}=ml\dot{\theta}^2+mg\sin \theta -Mg\\ l\ddot{\theta}=g\cos \theta -2\dot{l}\dot{\theta}$$

取初始条件

$$\left[ \begin{array}{c} l_0\\ \theta_0\\ \end{array} \right] =\left[ \begin{array}{c} 3\\ 0\\ \end{array} \right] ,\left[ \begin{array}{c} \dot{l}_0\\ \dot{\theta}_0\\ \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ \end{array} \right] ,\left[ \begin{array}{c} \ddot{l}_0\\ \ddot{\theta}_0\\ \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ \end{array} \right]$$

用数值（暴力）解法可以写出迭代式

$$\ddot{l}_i=\frac{ml_{i-1}\dot{\theta}_{i-1}^{2}+mg\sin \theta _{i-1}-Mg}{m+M}\\ \ddot{\theta}_i=\frac{g\cos \theta _{i-1}-2\dot{l}_{i-1}\dot{\theta}_{i-1}}{l_{i-1}}\\ \dot{l}_i=\dot{l}_{i-1}+\ddot{l}_i\Delta t\\ \dot{\theta}_i=\dot{\theta}_{i-1}+\ddot{\theta}_i\Delta t\\ l_i=l_{i-1}+\dot{l}_i\Delta t\\ \theta _i=\theta _{i-1}+\dot{\theta}_{i-1}\Delta t$$

这样就可以求解出位置关于时间的函数，绘制成动画如下