数值分析笔记
蛮有用的一门(尤其是做数学动画的时候),应该边写程序边上这门课。
误差部分

在对实际问题建模、计算时会有很多误差,这些方法有时候会变的很大,导致数据不可用。因此研究误差时数值计算的基本。
误差的来源
误差总共分为4类:系统误差、观测误差、截断误差、舍入误差
数值计算环节误差主要来源于 截断误差、舍入误差
误差的衡量
$x$为准确值,$x^❀$为近似值
- 绝对误差 $e(x) = x^❀-x$,
- 相对误差 $e_r(x) = {({x^❀}-x)/x}$,不过由于$x$无法算出,一般取$e_r(x)=({x^❀}-x)/{x^❀}$
- 有效数字$n:x^❀ = \pm10^m\times0.a_1a_2…a_n,|x-x^❀|\leq0.5\times10^{m-n+1}$
数值计算中的误差
$x=[x_1,x_2,…,x_n]^T$为准确解,$x^❀=[x^❀_1,x^❀_2,…,x^❀_n]^T$为近似值,$A^❀ = f(x^❀)$为误差
绝对误差$e(A) = A^❀-A=\sum\limits_{j=1}^n\frac{\partial f(x)}{\partial x_j}e(x_j)$
这里用到了Taylor展开取到一阶导
相对误差$e_r(A)=\frac{A^❀-A}{A}=\sum\limits_{j=1}^n\frac{x_j}{f(x)}\frac{\partial f(x)}{\partial x_j}e_r(x_j)$
注意$\partial f(x)/\partial x,\frac{x_j}{f(x)}\frac{\partial f(x)}{\partial x_j}$ 对误差的影响很大,后者成为条件数,当其值>10时,称该算法不稳定
防止误差过大方法
- 避免大数除小数
- 避免大数加小数
- 避免相近数相减
改变计算公式,可以去除这些。
插值与拟合部分
插值和拟合主要将一些离散的数值点用函数来表示。
插值
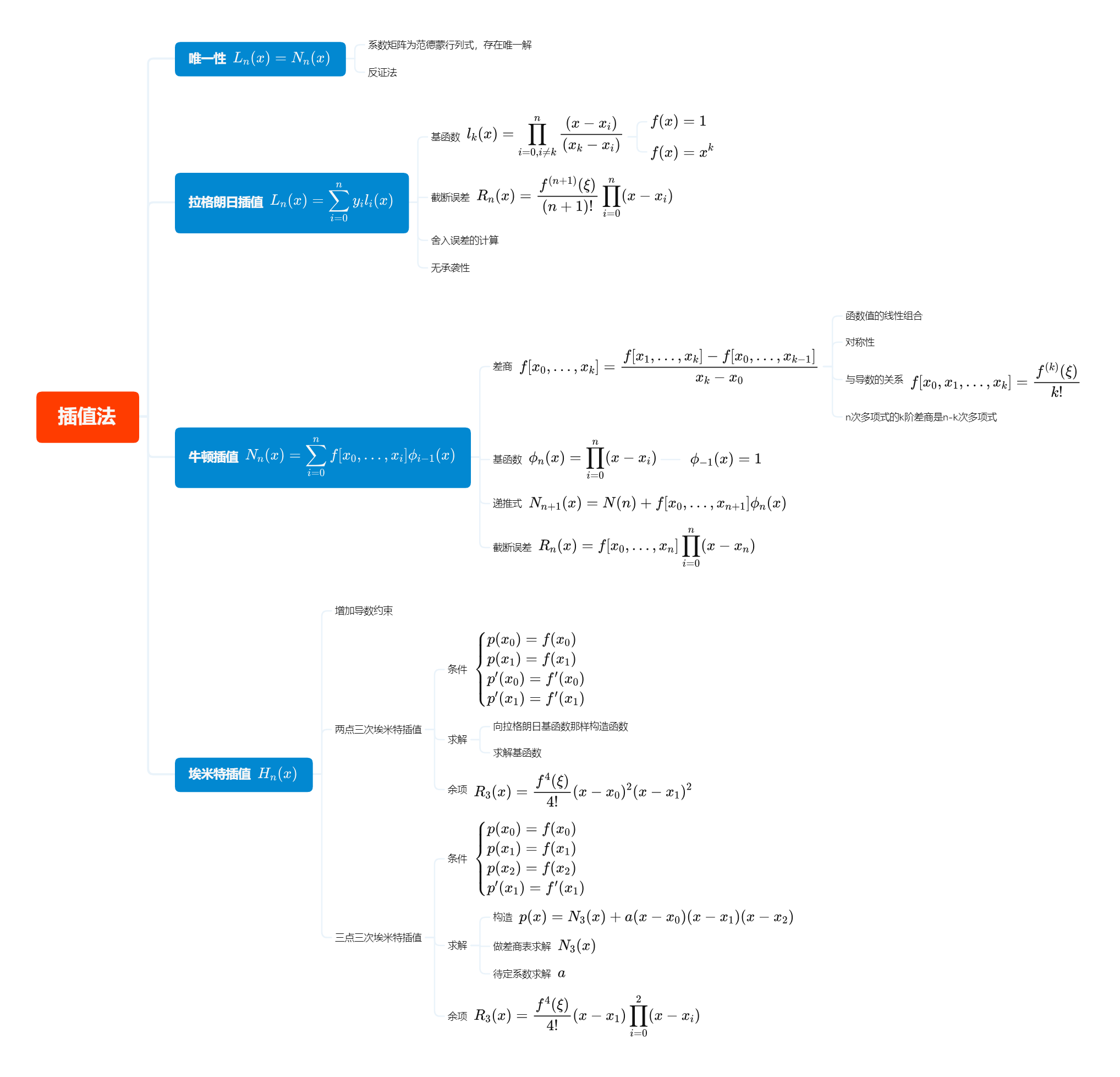
插值是在一些基函数的线性组合中找到一个函数$y=f(x)$,这个函数要经过每个数值点$y$。下面就只讨论多项式插值了:$f(x)=a_0x^0+a_1x^1+…+a_nx^n$
常见的基函数有多项式,三角函数。
插值函数的个数
对于(n+1)个节点,n 次插值多项式存在且唯一
证明:各个节点处建立方程,系数行列式为 范德姆行列式,存在且唯一(n+1个方程,n+1个未知数,因此存在且唯一)
如果两个式子次数相同为 n,且对所有(n+1)个节点式子成立,那么这两个式子相等
拉格朗日插值
插值函数的求解方法有很多。先说拉格朗日的方法:
为了满足那些数值点在函数上,就改写一下函数,同时改个名字为$L(x)$
这些$l(x)$就是需要构造的函数,目前还不知道。为了让点在$f(x)$上这个函数上,它满足下面的规律:
因此可以构造为:
这个就是拉格朗日插值基函数,其插值余项(截断误差)为
这个里面的$f(x)$为原始的要去插值贴近的函数。
在实际问题中,往往不知道$f(x)$的具体解析表达式,因此要估计$f^{(n+1)}(x)$的上界是不现实的。在这种情形下,可以采用误差的事后估计法:
其误差有以下特点:
- 对多项式插值,增加阶数不一定能提高精度
- 插值多项式仅与已知数据有关,与$f(x)$原来形式无关,但余项与$f(x)$密切相关
- 增加一个插值结点,所有的基函数都要重新计算。(没有沿承性)
牛顿插值
拉格朗日插值法没有沿承性,牛顿插值就是用来解决这个问题的。因此要构造
其中$a$为设的一常数,$q_{n+1}$是设的一函数,下面就需要构造$q_{n+1}(x)$,然后求解$a$
由于$N_{n+1},N_n$是插值多项式,因此在$x_0.x_1,…,x_n$上是相等的,根据上面那个式子,可以得到:$q_{n+1}(x_i)=0,i=0,1,…n$。根据这个性质,可以构造$q_{n+1}(x)=a_{n+1}\prod\limits_{i=0}^n(x-x_i)$
根据$q_{n+1}(x)$ 可以反推出$N_{n}(x)=a_0+a_1(x-x_0) + …+a_n(x-x_0)…(x-x_{n-1})$
将我们的节点带入,可以得到一堆方程:
(n+1)个方程,(n+1)个未知数,可以解出$a_i,i=0,1,…,n$的值。由于这个数字比较重要,我们把这些数字叫做差商,其表达式如下:
差商有很多重要的性质,比如说下面的:
- 0阶差商:$f[x_0]=f[x_0]$
k阶差商:$f[x_0,x_1,…,x_k]=\frac{f[x_0,x_1,…,x_{k-1}]-f[x_1,x_2,…,x_{k}]}{x_0-x_{k}}$
例如:1阶次差商:$f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0}$
交换差商节点的位置,差商的值没有变化(差商的对称性)
例如:$f[x_0,x_1,x_2]=f[x_1,x_0,x_2]$
差商除了用递归式写,还可以用迭代式表示:
差商和导数的关系可以由拉格朗日中值定理套娃给出:$f[x_0,x_1,…,x_k]=f^{(k)}(\xi)/(n!)$
其实差商可以想象成导数,只不过离散化了。
有了差商,牛顿插值多项式就构造出来了
余项(截断误差):$R_n(x)=f[x_0,x_1,…,x_n,x]\prod\limits_{i=0}^n(x-x_i)$
这个与拉格朗日插值的误差是一样的
拟合
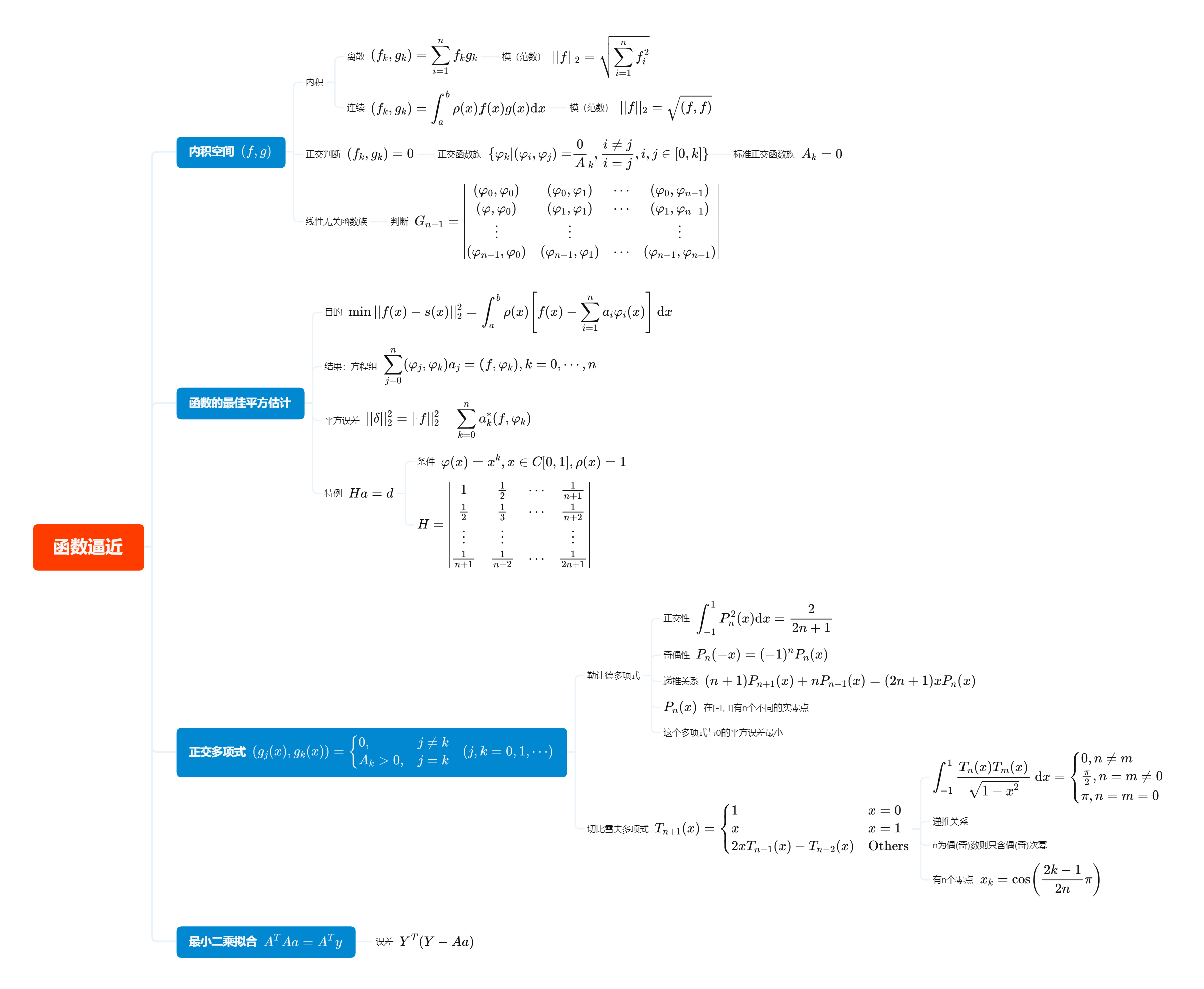
正则方程组
设有 n 个节点的拟合函数为 $y=a_0+a_1x+…+a_mx^m$ :
- $a_on+a_1\sum\limits_{i=0}^nx_i^{1+0}+a_2\sum\limits_{i=0}^nx_i^{2+0}+…+a_m\sum\limits_{i=0}^nx_i^{m+0}=\sum\limits_{i=0}^ny_ix_i^{0}$
- $a_o\sum\limits_{i=0}^nx_i^{0+1}+a_1\sum\limits_{i=0}^nx_i^{1+1}+a_2\sum\limits_{i=0}^nx_i^{2+1}+…+a_m\sum\limits_{i=0}^nx_i^{m+1}=\sum\limits_{i=0}^ny_ix_i^{1}$
- $a_o\sum\limits_{i=0}^nx_i^{0+2}+a_1\sum\limits_{i=0}^nx_i^{1+2}+a_2\sum\limits_{i=0}^nx_i^{2+2}+…+a_m\sum\limits_{i=0}^nx_i^{m+2}=\sum\limits_{i=0}^ny_ix_i^{2}$
- …
- $a_o\sum\limits_{i=0}^nx_i^{0+m}+a_1\sum\limits_{i=0}^nx_i^{1+2}+a_2\sum\limits_{i=0}^nx_i^{2+m}+…+a_m\sum\limits_{i=0}^nx_i^{m+m}=\sum\limits_{i=0}^ny_ix_i^{m}$
数值积分与微分
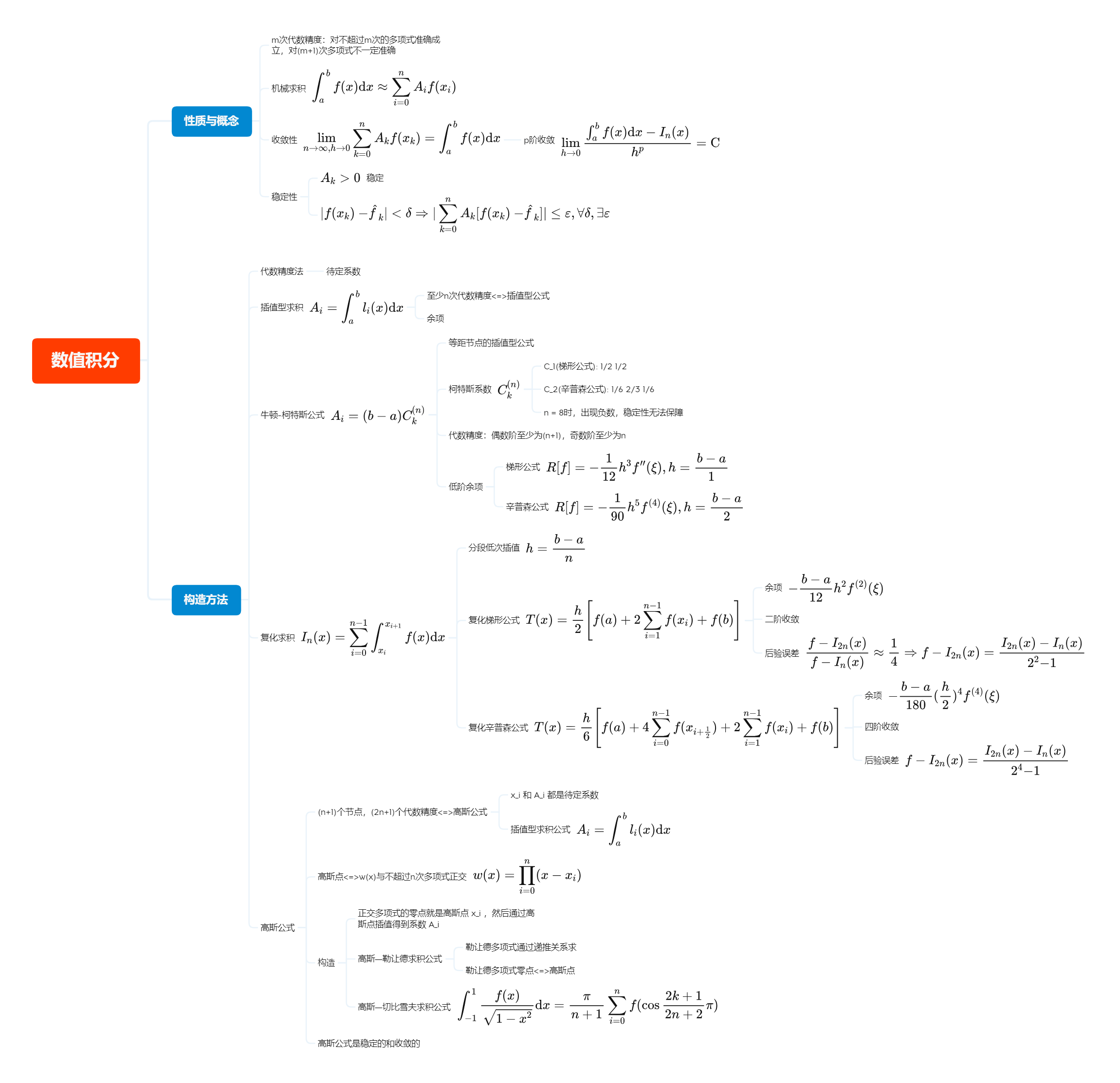
机械求积公式 $\int_a^bf(x)dx=\sum\limits_{i=1}^nA_if(x_i)$
机械求积公式余项 $R_n[f]=Kf^{(m+1)}(\xi)$ (m为代数精度)
其中 $K=\frac{1}{(m+1)!}[\int_a^bf(x)dx-\sum\limits_{i=1}^nA_if(x_i)]$ ,通常化简得 $K=\frac{1}{(m+1)!}[\frac{1}{m+2}(b^{m+2}-a^{m+2})-\sum\limits_{i=1}^nA_if(x_i)]$
中矩形公式 $\int_a^bf(x)dx=f(\frac{a+b}2)(b-a),R_n[f]=\frac{f^{(2)}(\xi)}{24}(b-a)^3$
梯形公式 $\int_a^bf(x)dx=\frac{f(a)+f(b)}2(b-a),R_n[f]=-\frac{f^{(2)}}{12}(b-a)^3$
辛普森公式 $\int_a^bf(x)=\frac{f(a)+4f[(a+b)/2]+f(b)}6(b-a),R_n[f]=-\frac{f^{(4)}}{2880}(b-a)^5$
插值型机械求积公式 $\int_a^bf(x)dx=\sum\limits_{i=1}^n\int_a^bl_i(x)dxf(x_i),R_n[f]=\int_a^b\frac{f^{(n+1)}(\xi)}{(n+1)!}\prod\limits_{i=0}^n(x-x_i)$
梯形法递推公式 $T_{2n}(h)=\frac12T_n(h)+\frac {h_n}2[\sum\limits f(x_{k+\frac12})]$
$S_n=\frac{4T_{2n}-T_n}3,C_n=\frac{16S_{2n}-S_n}{15},R_n=\frac{64C_{2n}-C_n}{63}$
高斯求积公式:在高斯求积公式中, 如果选择 n 个节点和求积公式,使其代数精度为 2m-1 ,这样的求积公式叫做高斯求积公式
通常令 $f(x)=1,x,x^2,…,x^k$ ,带入 $\int_a^bf(x)dx=\sum\limits_{i=1}^nA_if(x_i)$ 得到方程组,求解得到 $A_i,x_i$
两点高斯求积公式:$\int_{-1}^1f(x)dx=1\cdot f(\frac{-1}{\sqrt3})+1\cdot f(\frac{1}{\sqrt3})$
勒让德多项式 $P_n(x)=\frac{n!}{(2n!)}\frac{d^{n}}{dx^n}[(x^2-1)^n]$
- 正交性:$\int_{-1}^1P_n^2(x)dx=\frac{2}{2n+1}$,勒让德多项式对一切次数低于 n 次的多项式正交
- 奇偶性:n 为奇数,Pn(x) 为奇函数;n 为偶数,Pn(x) 为偶函数
- $P_n(\pm1)=\frac{(\pm 2)^nn!}{(2n)!}$
- 递推公式:$P_{n+1}(x)=xP_n(x)-\frac{n^2}{4n^2-1}P_{n-1}(x)$
- Pn(x) 的 n 个零点在(-1,1)上而且都是单根
向前差商:$f’(a)=\frac{f(a+h)-f(a)}{h}$ ;中间差商:$f’(a)=\frac{f(a+h)-f(a-h)}{2h}$
利用外推公式求导数$f’(a)$:
- 先用中间差商法求,得到一个关于 h 的函数:$f’(a)=\frac{f(a+h)-f(a)}{h}$ ,记为 G_0(h)
- 将步长二分,得到 G_0(h/2),等等
- 对 G_0(h) 进行修正,得到 G_1(h) = [4G(h/2) - G(h)] / 3
- 同理,得到 G_n
常微分方程数值解

线性代数方程组求解
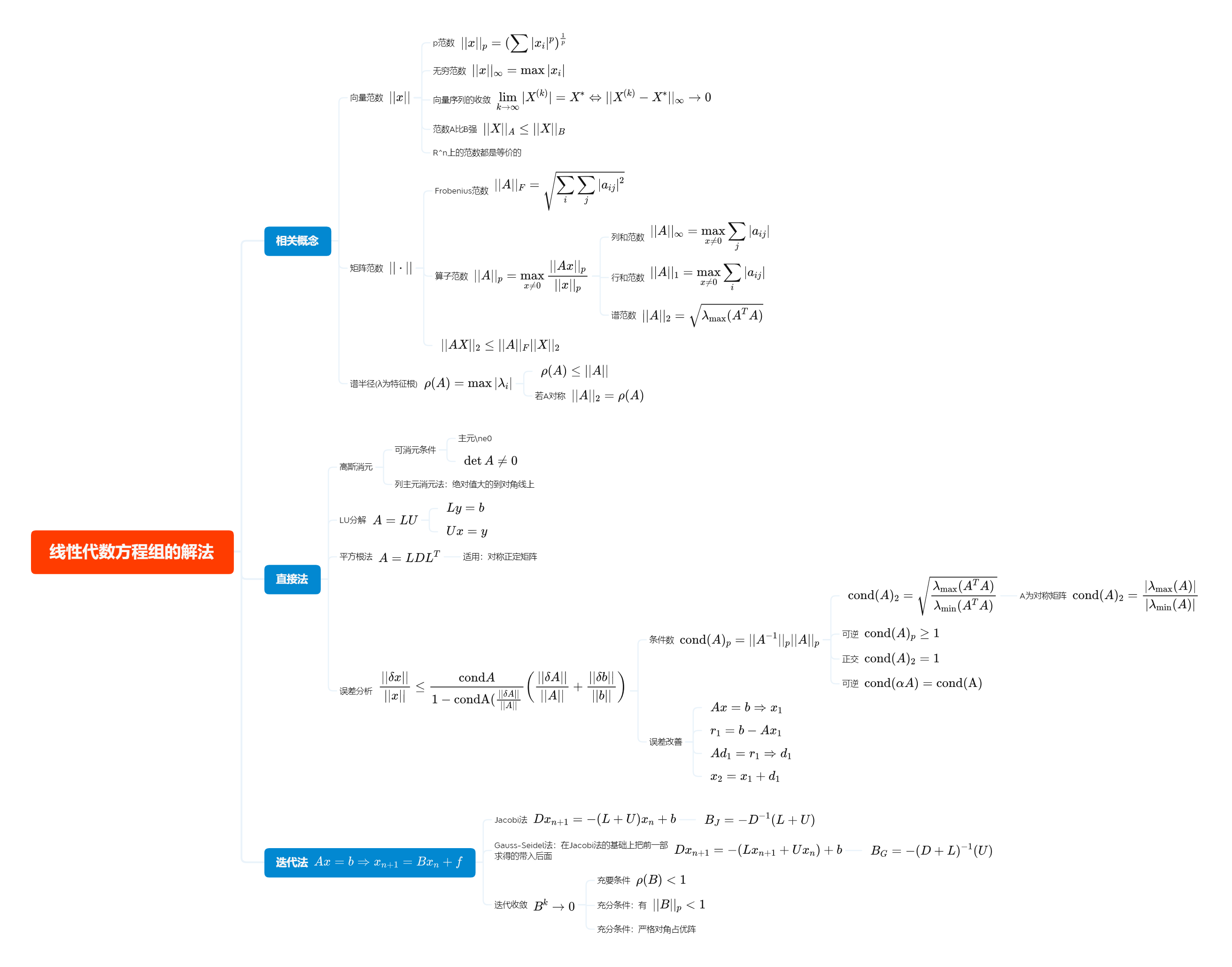
非线性方程求解

Learning By Sharing,2018-2020©Fu_Qingchen,Markdown,LaTeX