矩阵论笔记
矩阵论就是线性代数Plus,然后线性代数就是把一堆矩阵分解为一些简单的矩阵
线性代数复习
Review of Linear Algebra
常见的分解
Basic
- $A=CR=\left[ \begin{array}{c}\\\\\end{array} \right] \left[ \begin{matrix}&\\\end{matrix} \right]$ :将 A 分解为所有列都不相关的矩阵 C
- $A=LU=\left[\begin{matrix}{}\diagdown\ 0\\\ \ \ \ \ \ \diagdown\\\end{matrix} \right]\left[ \begin{matrix}{}\diagdown \ \ \ \ \ \\0 \ \diagdown\\\end{matrix} \right]$ :将 A 分解为上三角矩阵 U 和下三角矩阵 L
- $A=QR=\left[ \begin{matrix}|&|\\ \boldsymbol {q_1}&\boldsymbol{q_n} \\ |&|\end{matrix} \right]\left[ \begin{matrix}{}\diagdown \ \ \ \ \ \\0 \ \diagdown\\\end{matrix} \right]$ :将 A 分解为正交矩阵 Q ,其实跟第一个是一样的
- $S=Q\Lambda Q^T,Q^T=Q^{-1}$ :将一个对称矩阵 S 分解为正交矩阵 Q 和特征值 $\Lambda$ 组成的矩阵
- $A=X\Lambda X^T$:将方阵 A 分解为特征向量组成的矩阵 X 和特征值 $\lambda$ 组成的矩阵 $\Lambda$
- $A=U\varSigma V^T$:将矩阵 A 分解为正交向量组组成的矩阵 $U,V$ ($U^TU=V^TV=I$)和奇异值 $\sigma=\sqrt{\lambda(A^TA)}$ 组成的矩阵 $\varSigma$
矩阵的列空间
The column space of Matrixes
A的列空间 $C(A)$ :A中所有列向量的线性组合
$A=CR$
举例
对于一个 $m\times n$ 的矩阵 A,如果 A 中有 r 个线性无关的列向量,则可以分解为 $m\times r,r\times n$ 的两个矩阵 C 和 R。
C 的列向量就是那 r 个线性无关的列向量
R 的行向量包含 $r\times r$ 的单位矩阵 $I$ -> R 也线性无关
对 $A\boldsymbol x=\boldsymbol 0$ 来说,有 $n-r$ 个线性无关的解
- 秩为1的矩阵:如果 A 中所有的列都是第一列的倍数,那么 A 就可以分解为一个列向量和一个行向量
线性代数一览
The Big Picture of Linear Algebra
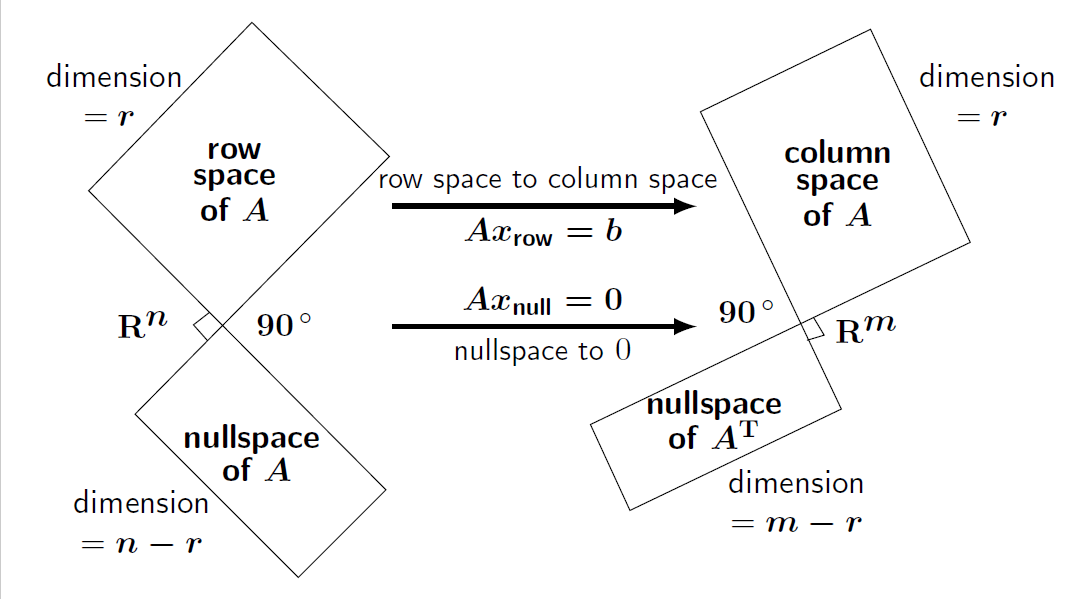
四个子空间
x 在 A 的零空间中,与 A 中的每一个行向量都不相关。$N(A)\perp C(A^T),N(A^T)\perp C(A)$
$N(A)$:所有使 $A\boldsymbol x=\boldsymbol 0$ 的向量张成的空间,$R^n$中维度为 $n-r$ 的空间
$C(A^T)$:A行向量张成的空间,$R^n$中维度为 $r$ 的空间
$N(A^T)$:所有使得 $\boldsymbol yA^T=\boldsymbol 0$ 的向量张成的空间,$R^m$ 中维度为 $m-r$ 的空间
$C(A)$:A列向量张成的空间,$R^m$ 中维度为 $r$ 的空间
矩阵乘法
有两种特殊的方法,有时候会算的快一些
$A=LU$
LU分解的一大作用就是解方程,这个分解只考虑行向量的加减和数乘运算,如果考虑行的交换,原式需要变为 $PA=LU$
这个分解来源于解方程 $Ax=b$
分解方法就是去逐行消元
求解$A\boldsymbol x=\boldsymbol b$
$A\boldsymbol x=\boldsymbol b$ 的通解可以分解为 $A\boldsymbol x =\boldsymbol 0$ 的通解加上 $A\boldsymbol x= \boldsymbol b$ 的特解
先求解 $A\boldsymbol x=\boldsymbol 0$ 的通解,初等行变换并不会改变矩阵的行空间, $N(A)=N(R)$
然后求解 $A\boldsymbol x=\boldsymbol b$ 的特解,$A\boldsymbol x =\boldsymbol b\Rightarrow R\boldsymbol x=\boldsymbol d$
正交向量
Orthogonal Vectors
- $Q^T=Q^{-1}$,对于单位正交矩阵,有 $Q^TQ=I$,注意 $QQ^T\ne I$
- $||Q\boldsymbol x||=\boldsymbol x^TQ^TQ\boldsymbol x=\boldsymbol x^T\boldsymbol x=||\boldsymbol x||$
应用:最小二乘法
当 $A\boldsymbol x=\boldsymbol b$ 无解,求解 $A^TA\boldsymbol x =A^T\boldsymbol b$ 可以得到最相近的
最小二乘法是数据很多时的一个曲线拟合,求解使 $\min(||A\boldsymbol x-\boldsymbol b||^2)$ 的 $\boldsymbol x$ ,其中 A 为 $m>n$ 的数据矩阵。然后可以将问题转化为求解 $\boldsymbol b$ 在 $ C(A)$ 上的投影 $\boldsymbol p$ 和 $A\boldsymbol x = \boldsymbol p$
直线上的投影
- $\hat x=(a^Tb)/(a^Ta)$: $a\perp(e=b-p)\Rightarrow a·(b-\hat xa)=0$
- $p=a\hat x=(aa^Tb)/(a^Ta)$
- $p=Pb\Rightarrow P=(aa^T)/(a^Ta)$
子空间投影
- $\hat x:A^T(b-A\hat x)=0\Rightarrow A^TAx=A^Tb$
- $p:p=Ax=A(A^TA)^{-1}A^Tb$
- $P:p=Pb\Rightarrow P=A(A^TA)^{-1}A^T$
最小二乘法
$A=QR$:Grant-Schmidt法
这里是将一个可逆矩阵转化为正交矩阵的方法。
方法就是把一个个列向量(基向量)减去已经正交化的向量的投影
- $a_1’=a_1,q_1=a_1’/||a_1’||$
- $a_i’=a_i-\frac{a_1^Ta_i}{a_1^Ta_1}a_1-\dots-\frac{a_{i-1}^Ta_i}{a_{i-1}^Ta_{i-1}}a_{i-1},q_i=a_i’/||a_i’||$
分解如下
特征值与特征向量
Eigenvalue and Eigenvectors
线性代数解方程是一大块,特征值与特征向量就是另外一大块内容了。
$S=Q\Lambda Q^T$
概念
对称矩阵:$S=S^T$
特征值 $\lambda$ 与特征向量 $\boldsymbol x$ :$A\boldsymbol x=\lambda\boldsymbol x$
所有特征值非负
对于对称矩阵 $S$,有
对称矩阵的特征向量是正交的,证明:
假设有 $S\boldsymbol x=\lambda \boldsymbol x,S\boldsymbol y=\alpha \boldsymbol y,\lambda\ne\alpha$
$\boldsymbol x^TS\boldsymbol y=(S^T\boldsymbol x)^T\boldsymbol y=(S\boldsymbol x)^T\boldsymbol y=\lambda\boldsymbol x^T\boldsymbol y$,$\boldsymbol x^TS\boldsymbol y=\boldsymbol x^T\alpha\boldsymbol y=\alpha \boldsymbol x^T\boldsymbol y$ $\Rightarrow\boldsymbol x^T\boldsymbol y=0$
正定矩阵:对所有 $\boldsymbol x>0$ , $\boldsymbol x^TS\boldsymbol x>0$
$A=X\Lambda X^{-1}$
上面那个式子更一般的情况,这个对有 $n$ 个线性无关特征值的方阵
$A^n=X\Lambda^nX^{-1}$
$\text{All: }|\lambda_i|<1,\Lambda^n\rightarrow0,A^n\rightarrow0$
特征向量与特征根的求解
设 $\lambda$ ,计算 $\det(A-\lambda I)$
求解使 $\det(A-\lambda I)=0$ 的特征值 $\lambda$
对每个 $\lambda$,求解使 $(A-\lambda I)\boldsymbol x=\boldsymbol 0$ 的特征向量 $\boldsymbol x$
其他的
矩阵相似:特征值相同的两个矩阵相似 $\text{All } A=BCB^{-1}\sim C$
$\det(A)=\prod\lambda_i$
$\sum a_{ii}=\text{trace}=\sum\lambda_i$
奇异值与奇异矩阵
Singular values and Singular vectors
特征值和特征向量是对于方阵而言的,奇异值和奇异矩阵是对非方阵而言的。
$A=U\varSigma V^T$
$A^TA\boldsymbol v_i=\sigma_i^2\boldsymbol v_i,AA^T\boldsymbol u_i=\sigma^2_i\boldsymbol u_i,A\boldsymbol v_i=\sigma\boldsymbol u_i$
$A^TA=(V\varSigma^T U^T)U\varSigma V^T=V\varSigma^2$
$AA^T=U\varSigma V^T(V\varSigma^TU^T)=U\varSigma^2U^T$
$AV=U\varSigma,V^TV=U^TU=I$
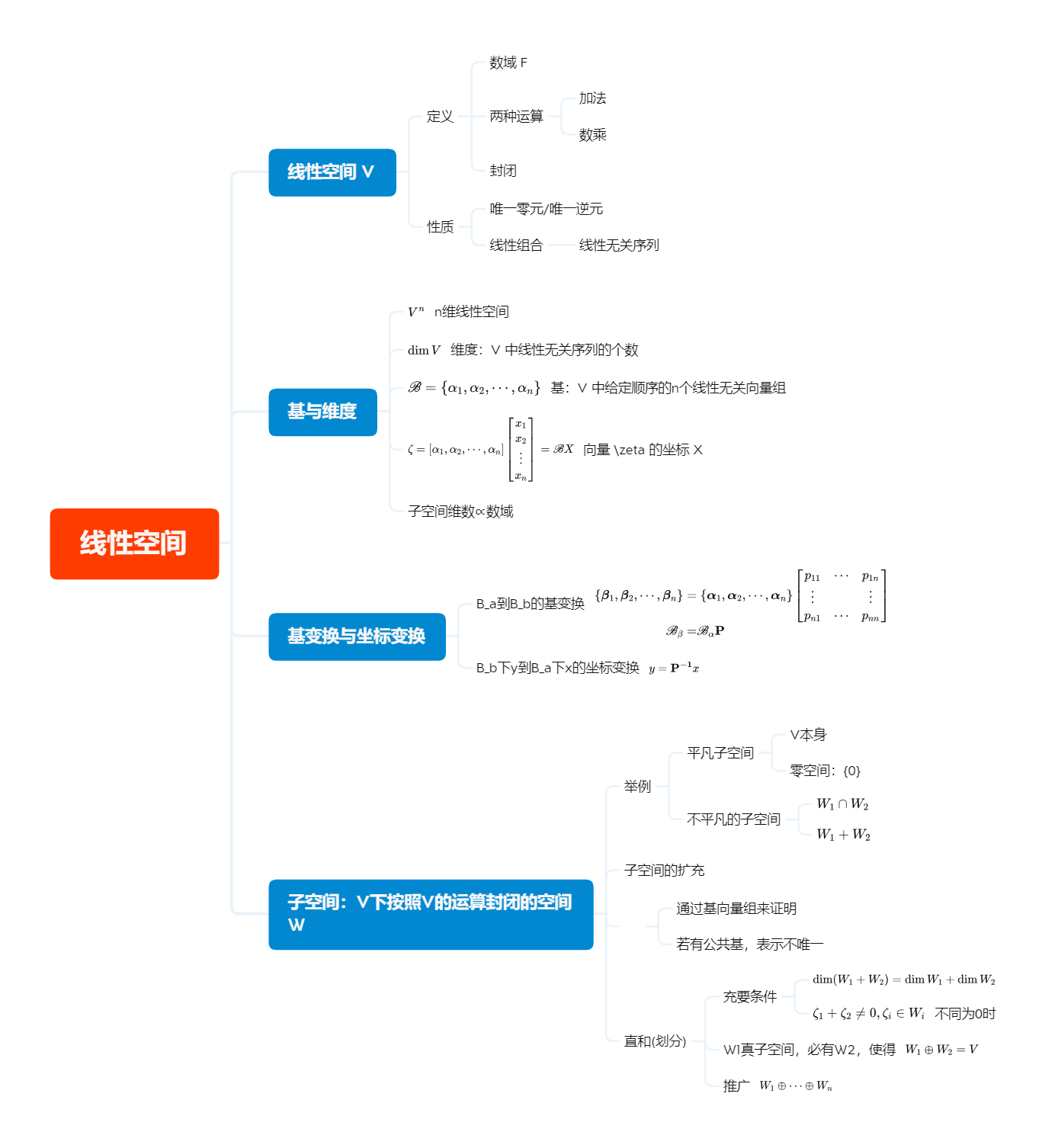
线性空间与线性变换
线性空间
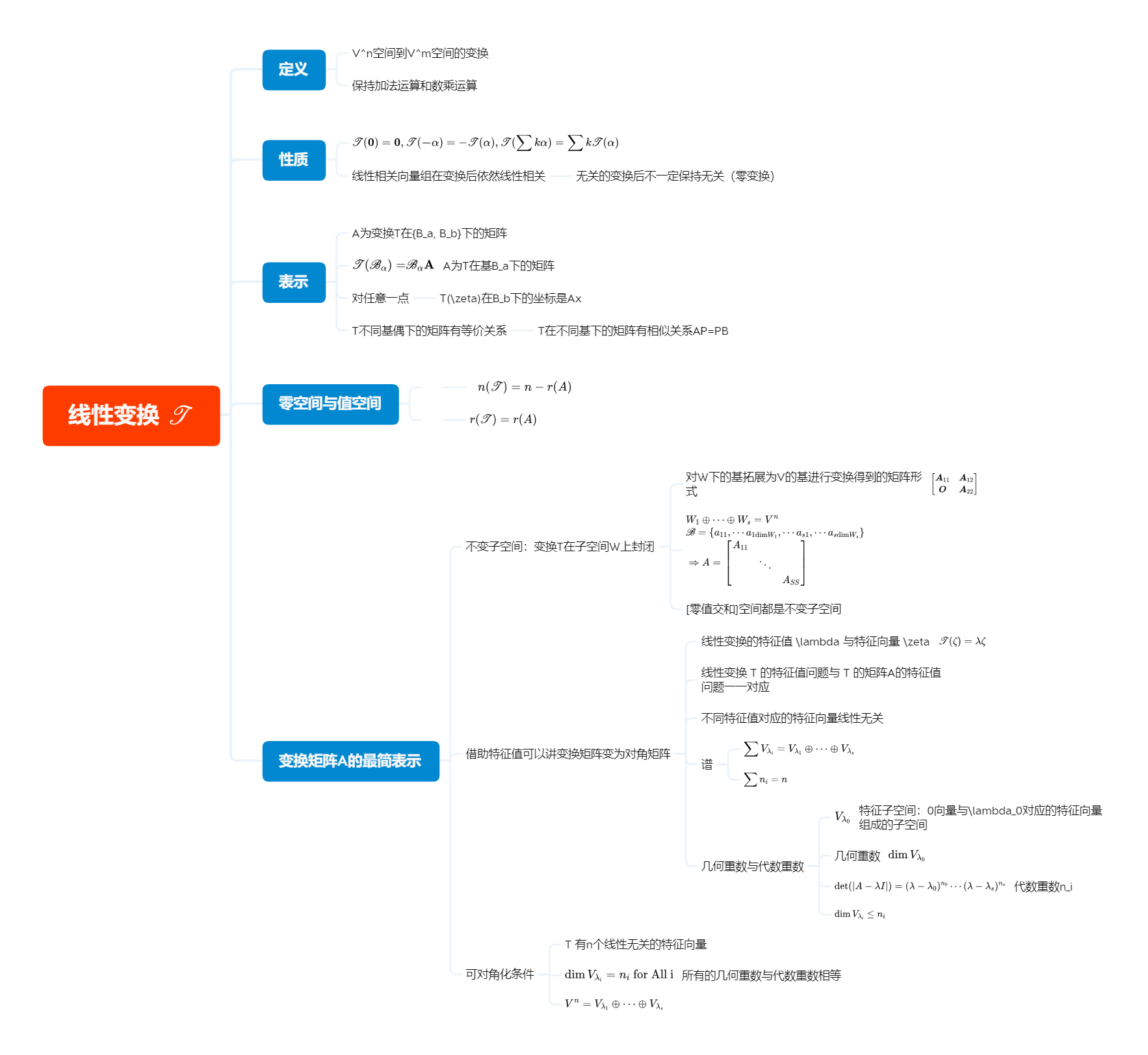
线性变换
矩阵的相似化简
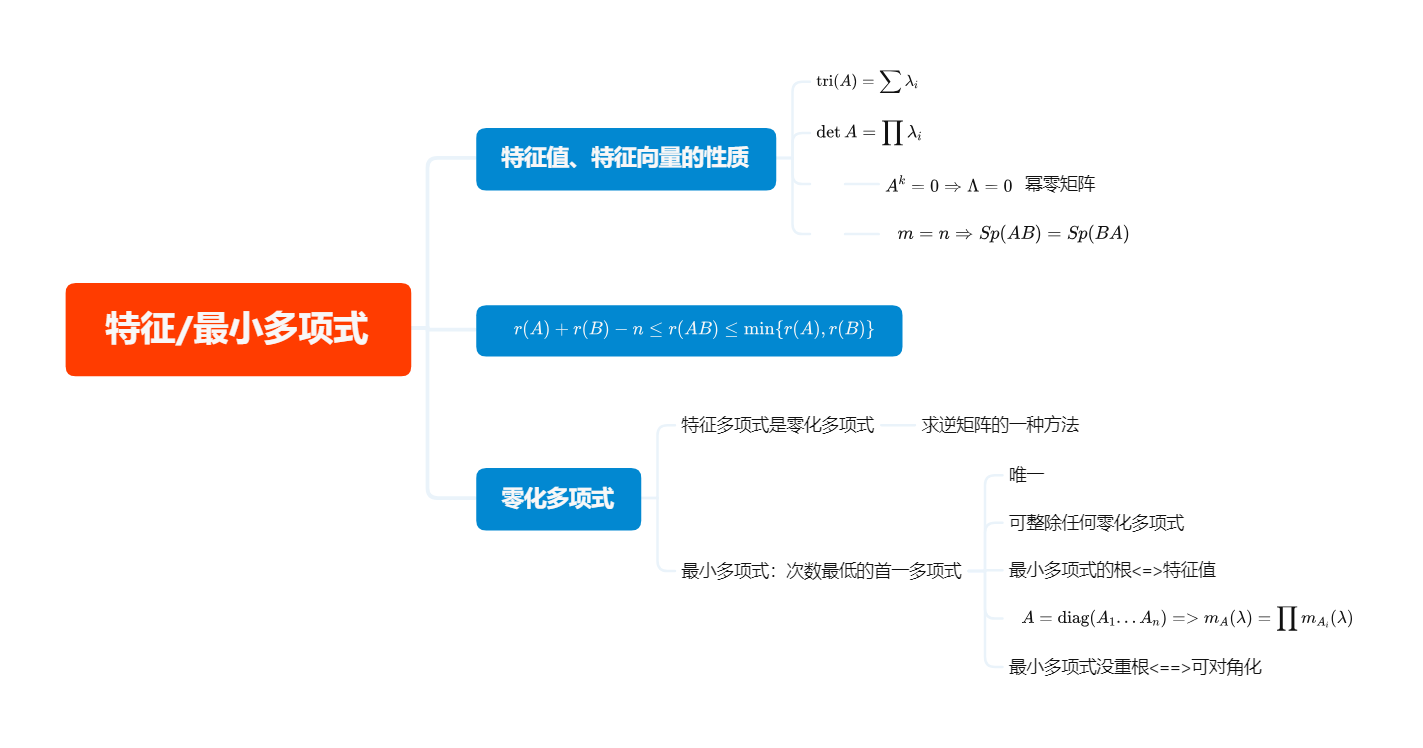
特征多项式与最小多项式
Jordan标准型

2020©Fu_Qingchen, LearningBySharing