数据结构与算法

数据结构更新至绪论，算法更新至堆排序。

作为计算机基础4大件，数据结构与算法是讲如何让计算机算的对，算的快，能让我们高效的使用计算机。

正在进行

绪论

• 程序 = 算法 + 数据结构
• 一个好算法
  • 正确
  • 高效
  • 鲁棒（能辨别不良数据，并且进行优化，不非正常退出）
  • 可读

评价算法

方法&环境

• 实验（最直接，但是不可行，因为不太方便在同一尺度下比较）

• 图灵机模型

  

  • 组成：无限长纸带、有限字母表、有限状态信息、读写头
  • 转换函数：Transition Function = (图灵机当前状态, 当前字符; 修改后的字符, 下一步前进方向, 图灵机改变后的状态)

• RAM模型

  • 无限储存空间
  • 计算时间∝计算次数

指标

计算规模小的问题很快就会解决，因此只用考虑足够大的问题。

只考虑算法运算时间随时间的增长率（采用渐进分析）

• 大O记号（上界, 悲观估计）

• 其他记号：Θ（同增长率），Ω（上界）

• 常见的时间复杂度

  • 常数复杂度$O(1)$
  • 对数复杂度$O(\lg n)$
  • 多项式复杂度$O(n^c)$（线性复杂度）
  • 指数复杂度$O(2^n)$

• 一些常见求时间复杂度的公式

  • $\sum\limits_{i=1}^ni^d=O(n^{d+1})$
  • 几何级数与其自身同阶$\sum\limits_{i=0}^na^n=O(a^n)$
  • $\sum\limits_{i=1}^ni^{-1}=O(\lg n)$
  • $\sum\limits_{i=1}^n\lg i=O(n\lg n)$

例如

for(int i = 0; i <= n; i++){
	for(int j = 0; j < i; j+=j){
        ...
       }
}

有$\sum\limits_{i=1}^n\lg i=O(n\lg n)$的时间复杂度

快速估计：封底估算

抓住主要问题进行估计

迭代与递归

• 空间复杂度：除输入外所需附加的空间

• 减而治之：逐步的减小问题的规模

• 分而治之：划分成两个规模相当的子问题

• 递归分析方法

  • 递归跟踪：直观、形象，仅适用于简答的递归模式

    把递归的函数一条条列出来，分析其中的逻辑

  • 递推分析：间接、抽象，适用于复杂的情况

    把递归式子写成数学归纳法的样子，然后解微分方程

动态规划

递归用到函数调用，效率会比较低，动态规划就是将递归变成迭代的

数据结构 | Data Structure

主要介绍实现方式，重点是STL的实现方式

向量 | Vector

向量就是数组的拓展，让它配合向量ADT接口。向量是一种线性结构，其物理位置与逻辑位置完全相同，可以执行高效的静态操作，如实现$O(1)$的寻秩访问。

std::vector 的底层实现为线性连续数组。 std::vector 的核心问题是扩容。最开始 std::vector 的容量为 0 ，插入一个元素后容量为 1，随后每次乘二（size = 16, capacity = 16）

graph LR
Vector-->属性-->_size
属性-->_capacity
属性-->_elem
Vector-->操作-->构造类操作
构造类操作-->构造函数/析构函数
构造类操作-->复制构造函数
构造类操作-->动态空间管理-->expand-->加倍策略
expand-->分摊时间复杂度
构造类操作-->insert/remove
动态空间管理-->shrink
操作-->查找类操作-->寻秩访问
查找类操作-->无序-->find
无序-->deduplicate
查找类操作-->有序-->search
有序-->uniquify
操作-->排序类操作
search-->二分查找
search-->Fibonacci查找
search-->插值查找

列表 | List

列表是另外一种线性的数据结构，与向量不同的是，它物理位置与逻辑位置不完全相同，可以执行高效的动态操作，寻秩访问速度较慢，主要进行的是寻位访问。

std::list 为双向列表，forward_list 为单向列表

列表是基于结点的数据结构，其结点至少包含前驱指针、后继指针和数据三个数据。

graph LR
node-->A(属性)-->pred/succ
A-->data
node-->B(操作)-->insertAfter/insertBefore
List-->C(属性)-->_size
C-->header/trailer
List-->D(操作)-->寻秩访问/寻位访问
D-->构造/析构/基于复制的构造
D-->insert/remove/deduplicate/traverse
D-->uniquify/search
D-->排序-->选择排序
排序-->插入排序

双端队列 | Deque

std::vector 只能实现高效的从尾部插入数据，而双端队列则可从首尾插入数据

std::deque 的实现是动态的由多段连续空间组合而成。std::deque 的主体是一个指针数组，数组中的每一个节点都指向对应的一块连续的内存空间，这个里面存放的就是数据了。std::deque 有一个map_size 用来记录指针数组有多少个指针，有start, end 两个迭代器记录起始位置和数据结束的位置。

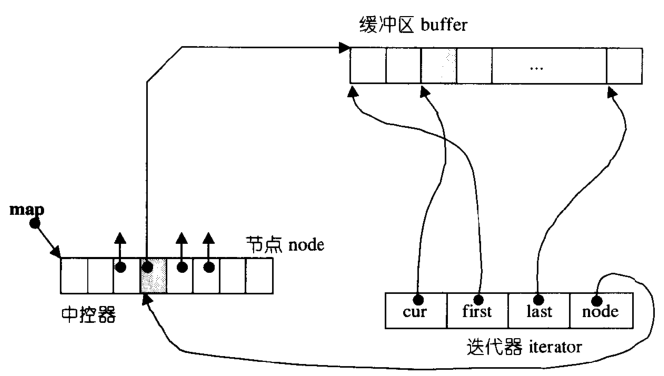
中控器就算对应的指针数组，缓冲区就算指针数组中指向的连续的内存区域

std::deque 的迭代器有4个对象

• cur ：用于指向迭代器所指元素。
• first & last ：指向当前缓冲区的头与尾。
• node ：指向中控器中指向本缓冲区的指针。

由于 std::deque 本身结构比较复杂，它的迭代器也不是普通的指针，因此能使用std::vector就尽量使用std::vector

栈和队列 | Stack & Queue

栈和队列就是向量和列表的特例，其中栈讲究先入后出，队列讲究先入先出。

graph LR
Stack-->属性-->size
Stack-->操作-->push
操作-->pop/top
Stack-->应用-->逆序输出
应用-->延迟缓冲
应用-->递归嵌套-->括号识别
递归嵌套-->栈混洗
应用-->栈式计算-->RPN
栈式计算-->中缀表达式

graph LR
Queue-->enqueue/rear
Queue-->dequeue/front

std::stack, std::queue 是由其他容器构造出的，因此叫做容器构造器。默认情况下 std::stack, std::queue 利用 std::deque 实现,

算法 | Algorithm

排序| Sorting

冒泡排序

思路：遍历数组，将数组的前一个元素和后一个元素进行比较，让大的数放在后面。一次遍历完成之后，最大的数就在最后了。然后在对当前数组的 [0,size-1) 部分进行冒泡排序

template<typename T>
void bubbleSort(vector<T> &data) {
    int size = data.size();
    for (int i = size - 1; i >= 0; --i) {
        bool flag = true;
        for (int j = 0; j < i; ++j) {
            if (data[j] >= data[j + 1]) {
                swap(data[j], data[j + 1]);
               	flag = false;
            }
        }
        if(flag) { return ; }
    }
}

选择排序

思路：遍历数组，选择其中最小的那个与数组第一个数交换，然后对数组的 [1:size) 部分进行排序

template<typename T>
void selectionSort(vector<T> &data) {
    int size = data.size();
    for (int i = 0; i < size; ++i) {
        int minIndex = i;
        for (int j = i + 1; j < size; ++j) {
            if(data[j] < data[minIndex]) { minIndex = j; }
        }
        swap(data[i], data[minIndex]);
    }
}

插入排序

思路：1个元素开始，每次增加一个元素，让这个元素前的数组[0:i] 变成有序的。具体的实现就第 i 个元素向前移动，移动到它前面的数都不大于它

template<typename T>
void insertionSort(vector<T> &data) {
    int size = data.size();
    for (int i = 1; i < size; ++i) {
        int currNum = 1;
        int currIndex = i;
        while(currIndex > 0 && data[currIndex] < data[currIndex - 1]) {
            if(data[currIndex] < data[currIndex - 1]) {
                swap(data[currIndex], data[currIndex - 1]);
            }
            --currIndex;
        }
    }
}

希尔排序

插入排序对有序的数组效率比较高，希尔排序是利用这一点对插入排序进行优化

思路：将数组按间隔进行分组，在每一组内进行插入排序，提高数组的有序程度，然后逐渐减少分组的间隔，直到间隔为1，排序完成

template<typename T>
void shellSort(vector<T> &data) {
    int size = data.size();
    for (int gap = size >> 1; gap > 0; gap >>= 1) {
        for (int i = 0; i < gap; ++i) {
            for (int j = i; j < size; j += gap) {
                // 下面是插入排序的部分
                int currIndex = j;
                while(currIndex > gap && data[currIndex] < data[currIndex - gap]) {
                    if(data[currIndex] < data[currIndex - gap]) {
                        swap(data[currIndex], data[currIndex - gap]);
                    }
                currIndex -= gap;
                }
            }
        }
    }
}

快速排序

思路：快速排序需要设定一个轴，然后把数组中小于轴的元素移到轴左边，大于轴的元素移动到轴的右边，然后轴左右两边的数组就成了一个子问题，递归的解决就可以了。

template<typename T>
void quickSort(vector<T> &data, int left, int right) {
    if(right <= left) { return; }
    T key = data[left];
    int i = left, j = right;
    while (i < j) {
        while (i < j && key <= data[j]) { --j; }
        swap(data[i], data[j]);
        while (i < j && data[i] <= key) { ++i; }
        swap(data[i], data[j]);
    }
    quickSort(data, left, i - 1);
    quickSort(data, i + 1, right);
}

归并排序

思路，把数组分为两个部分，然后递归的解决，得到两个已经排好序的数组，然后依次取两个子数组中最小的那个

template<typename T>
void mergeSort(vector<T> &data, int left, int right) {
    if(left + 1 >= right) { return; }
    int mid = (left + right) >> 1, size = right - left, l = left, r = mid;
    mergeSort(data, left, mid);
    mergeSort(data, mid, right);
    vector<int> temp(size);
    for(int i = 0; i < size;) {
        if((r >= right) || (l < mid && data[l] < data[r])) { temp[i++] = data[l++]; }
        if((l >= mid) || (r < right && data[l] >= data[r])){ temp[i++] = data[r++]; }
    }
    for(int i = 0; i < size; ++i) { data[left + i] = temp[i]; }
}

堆排序

思路：参见灯神的视频

template<typename T>
void heapify(vector<T> &data, int index, int size) {
    int lc = 2 * index + 1, rc = 2 * index + 2, max = index;
    if((lc < size) && data[lc] > data[max]) { max = lc; }
    if((rc < size) && data[rc] > data[max]) { max = rc; }
    if(index != max){
        swap(data[max], data[index]);
        heapify(data, max, size);
    }
}
template<typename T>
void buildHeap(vector<T> &data) {
    int size = data.size();
    for (int i = size >> 1 - 1; i >= 0; --i) { heapify(data, i, size); }
}
template<typename T>
void heapSort(vector<T> &data, int left, int right) {
    int size = data.size();
    buildHeap(data);
    for (int i = size - 1; i > 0; --i) {
        swap(data[0], data[i]);
        heapify(data, 0, i);
    }
}

计数排序

适用于数据量很大，但是数据返回很小

思路：记录每种元素数量的大小

void countSort(vector<int> &data) {
    int size = data.size(), index = 0, min = data[0], max = data[0];
    for (auto item : data) {
        min = item < min ? item : min;
        max = item > max ? item : max;
    }
    vector<int> valueCount(max - min + 1, 0), datacpy(data.begin(), data.end());
    for(auto item : datacpy) { ++valueCount[item - min]; }
    for (int i = min; i <= max; ++i) {
        while (valueCount[i - min]--) { data[index++] = i; }
    }
}

桶排序

把数据缩小范围，然后组内进行排序

计数排序和基数排序都是桶排序的一种

基数排序

多关键字的排序

例如对整数进行排序，