机械有限元分析笔记
这玩意好难,对材料力学和线性代数的基础要求很高,而且APDL对新手来说也很不友好。这个在毕业设计的时候也涉及到了,不过用的是Workbench,方便很多。
基础理论
有限元分析步骤
离散化结构:把连续结构的力学模型转变为离散的力学模型
单元分析:求出表示各个单元力学特性的单元刚度矩阵
- 整体分析:将各单元刚度矩阵组集成整个结构的总刚矩阵,引入边界条件,求解
有限元概念
设置节点的原则
- 同一单元内,单元的各项特性数据和材料数据应该保持一致
- 在载荷突变处,集中载荷作用点要设置节点
- 欲知道单元应力状况、位移状况、内力状况的地方要设置节点
形函数及性质
其中 $a_i=\left|
\begin{matrix}
x_j&y_j\\
x_m&y_m\\
\end{matrix}
\right|,b_i=-\left|
\begin{matrix}
1&y_j\\
1&y_m\\
\end{matrix}
\right|c_i=-\left|
\begin{matrix}
x_j&1\\
x_m&1\\
\end{matrix}
\right|$
单元内任意一点的三个形函数之和恒等于1。$N_i+N_j+N_m=1$
在 i,j,m 三个顶点处,有
在 i 节点处:$N_i=1,N_j=N_m=0$
在 j 节点处:$N_j=1,N_i=N_m=0$
在 m 节点处:$N_m=1,N_j=N_i=0$
位移模式收敛性分析
完备性
充分条件
位移模式需包括常应变状态
即应变分量 $\{\varepsilon\}$ 与 x,y 无关
位移模式需包括单元的刚体位移
即应变分量 $\{\varepsilon\}=0$ 时的位移方程,要和质点做刚体运动的方程对应
协调性
必要条件
位移模式必须反映位移的连续性
各个单元在变形之后单元内、单元间保持连续,不撕裂,不侵入
载荷的移置
原则是原载荷在任何虚位移上做的虚功,与移置到各节点的力所做的虚功相等
对于三角形三节点单元:
- 集中力的移置:$\{R\}=[N]^T{\{P\}}$ ,其中 $\{P\}$ 为集中力
- 面力的移置:$\{R\}=\int[N]^T\{p\}ds$ ,其中 $\{p\}$ 为面力密度
- 体力的移置:$\{R\}=\int[N]^T\{p\}tdxdy$ ,其中 $t$ 为厚度
对于轴对称单元:
- 集中力的移置:$\{R\}=2\pi r[N]^T{\{P\}}$ ,其中 $\{P\}$ 为集中力
- 面力的移置:$\{R\}=\int2\pi r[N]^T\{p\}ds$ ,其中 $\{p\}$ 为面力密度
- 体力的移置:$\{R\}=\int2\pi r[N]^T\{p\}drdz$ ,其中 $t$ 为厚度
总刚组集
原则
- 变形后各节点任然协调的相互连接(连续性)
- 各节点满足静力平衡条件,节点力 = 外载荷
步骤
扩大各单元矩阵,使之成为与总刚矩阵相同的阶数
此处的阶数 = 位移分量个数 × 节点数
按照总刚矩阵的编号,移动各单元矩阵的各个子块
- 将各个矩阵相加
总刚性质
位置无关性(总刚与位置无关,只与材料特性、几何形状、尺寸大小有关)
对称性
奇异性( $[K]$ 无逆矩阵,即在 $\{F\}=[K]\{\delta\}$ 只能由位移求力,不能由力求位移)
稀疏性(总刚中0多,非0少)
带状性(只有中间有数值,呈带状,两边都是0)
半带宽值 B = ( 相邻节点最大差值 + 1 ) × 单个节点自由度数(对平面问题,单个节点自由度数 = 2)
半带宽值与计算机处理性能有关,可越小越好
总刚矩阵的内存压缩机制
总刚矩阵具有对称性,只需存入主对角线上半带或下半带的元素,就可以完成解方程的运算。此即为总刚矩阵的半带宽存储方法。
假定取主对角线上半带元素存储,具体做法就是每行元素以主对角线上的元素开始,存储每行半带宽数值的元素个数。如此各元素的行号不变,改变的只是列号。新列号和原列号的关系式如下:
新列号 = 原列号 - 行号 + 1
总体边界条件的引入
边界节点固定
$u_{i}=u_{j}=0$
使用 置0-1法 :
即首先在总刚矩阵 $[K]$ 中与已知位移分量相对应的行和列元素改为 0,但主对角线上的元素改为 1 ,然后在节点载荷向量的列阵中,与已知对应元素的位移用代替,其余元素减去已知位移分别乘 $[K]$ 中相应元素。
边界有特定位移值
$u_{i}=C$
使用 乘大数法 :
在总刚矩阵 $[K]$ 中,把与已知位移位移相对应的行与列主对角线上的元素乘一个很大的数 $10^{10}$ ,然后把载荷向量中的对应元素代以给定位移乘以相应主对角线上的元素,再同样乘以一个很大的数。
应力平滑处理
由于三角形单元求得的应力或应变是不连续的,为了使模拟更加准确,因此要平滑应力的突变。
就是将绕某一节点的各单元形心应力加以平均,来表示该节点的应力。
常见单元类型

命令流
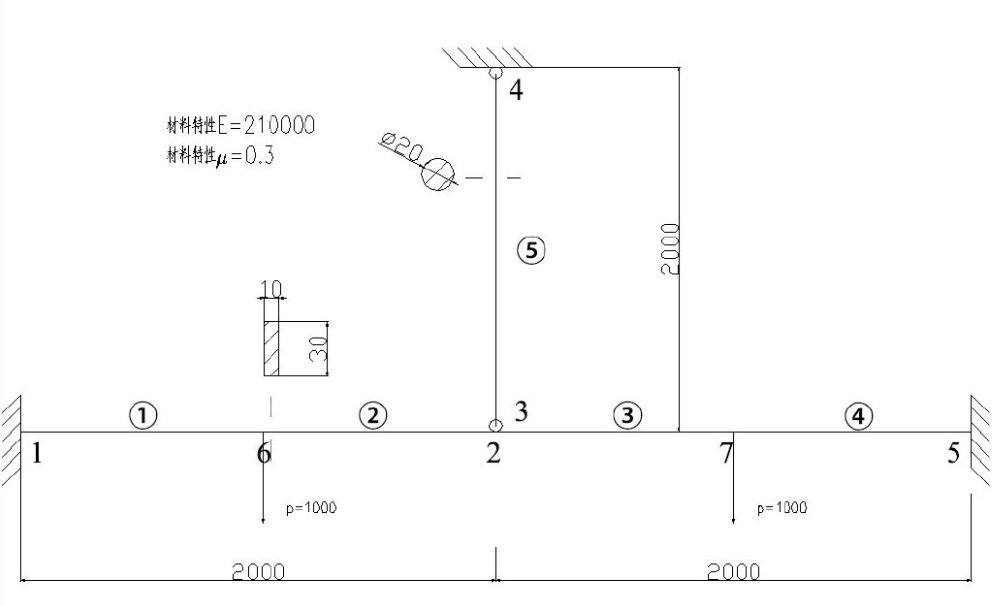
1 | |
Learning By Sharing,2018©Fu_Qingchen,Markdown,$\LaTeX$