控制工程基础笔记
这本课程比较考验数学,里面涉及到大量复变函数的概念和应用。
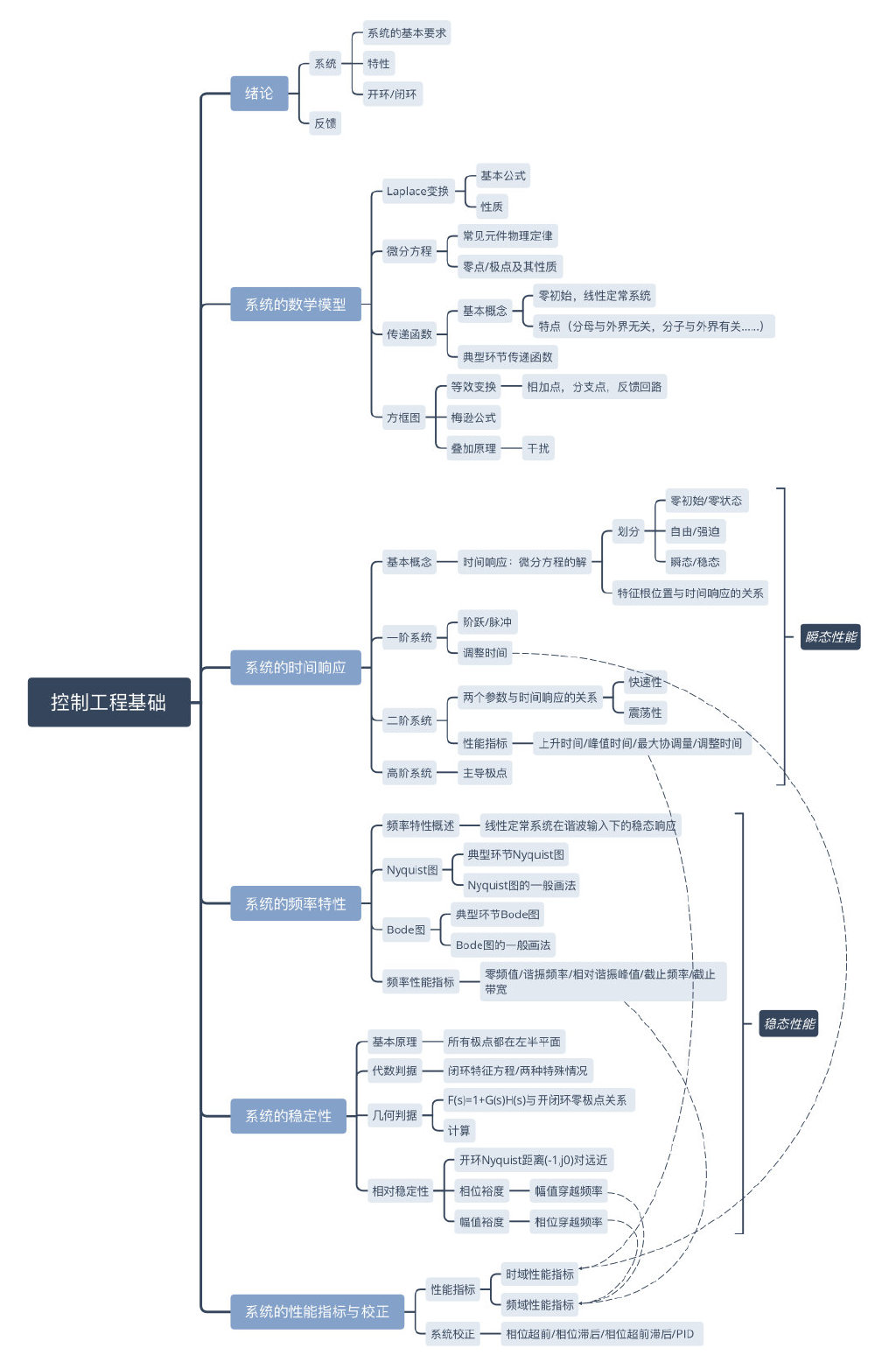
Introduction //绪论
机械控制工程实质:研究机械工程技术广义系统中的动力学问题
系统的性能不仅与系统的元素有关,还与系统的结构有关
- 系统往往在时域、频域或空域等域内表现出动态特性
- 对机械系统,系统的输入与输出分别称为 “激励” 和 “相应”
- 开环系统:没反馈回路的系统
- 特点:结构简单,成本低
- 闭环系统:有反馈回路的系统
- 对控制系统的基本要求:快、准、稳
Mathematical models //数学模型
Laplace Transform
Definition:
Typically Laplace Transform
unit impulse //单位阶跃
unit step//单位斜坡
unit impulse //单位脉冲
Properties of Laplace Transform //拉普拉斯变换的性质
Under the Zero state response:
应该就这些了。。。
Laplace变换的起源:
Mathmatical Model
- 微分方程是在时域中描述系统动态特性的数学模型
- 传递函数是在复域中描述系统动态特性的数学模型
- 线性定常系统:$\ddot x_o(t)+3\dot x_o(t)+x_o(t)=4\dot x_i(t)+5x_i(t)$
- 线性时变系统:$\ddot x_o(t)+3t\dot x_o(t)+x_o(t)=4\dot x_i(t)+5x_i(t)$
- 非线性系统:$\ddot x_o(t)+3x_o\dot x_o(t)+x_o(t)=4\dot x_i(t)+5x_i(t)$
典型元件微分方程
机械系统
- 质量元件:$f=m\ddot x,T=J\ddot\theta$
- 弹性元件:$f=kx,T=k\theta$
- 阻尼元件:$f=c\dot x,T=c\dot\theta$
电网系统
- 电容:$u=\frac1C\int idt$
- 电感:$u=L\frac{di}{dt}$
- 电阻:$u=Ri$
Transfer Function
零初始条件
线性定常系统
- 系统输出的Laplace变换与系统输入的Laplace变换之比
For a general n^{th}-order linear ,time invariant differential equation:
The Transfer Function is
- 传递函数的分母与外界无关,分子反映与外界的关系
- 相似系统传递函数相同
传递函数的零极点模型
$z_1,z_2…$ : 零点;$p_1,p_2$: 极点;$K$: 开环增益
系统的零点、极点对系统动态性能有影响,其中:零点影响系统的瞬态性能,极点影响系统的稳态性能
对系统的研究可以转化为对零点、极点、开环增益的研究
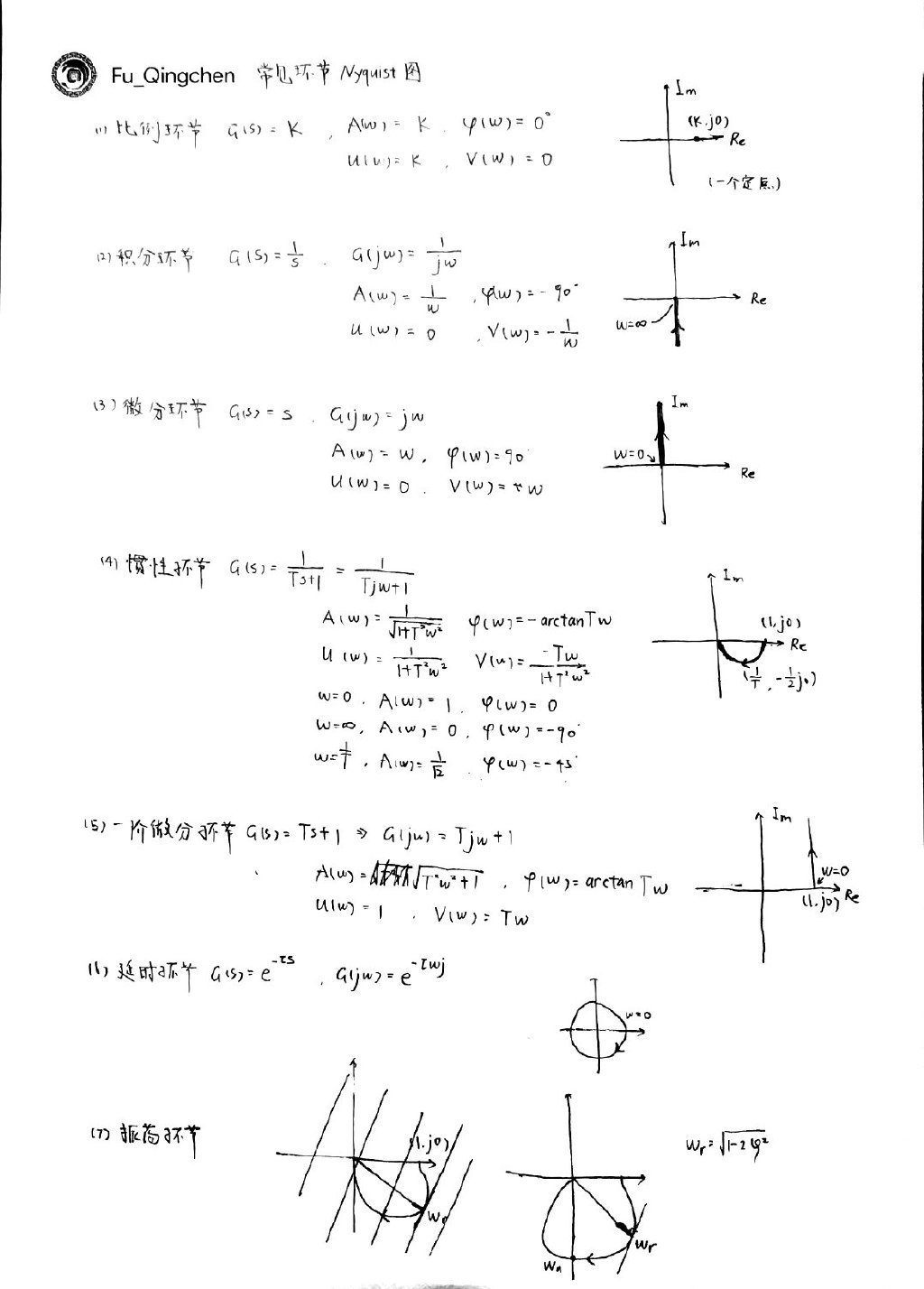
典型环节传递函数
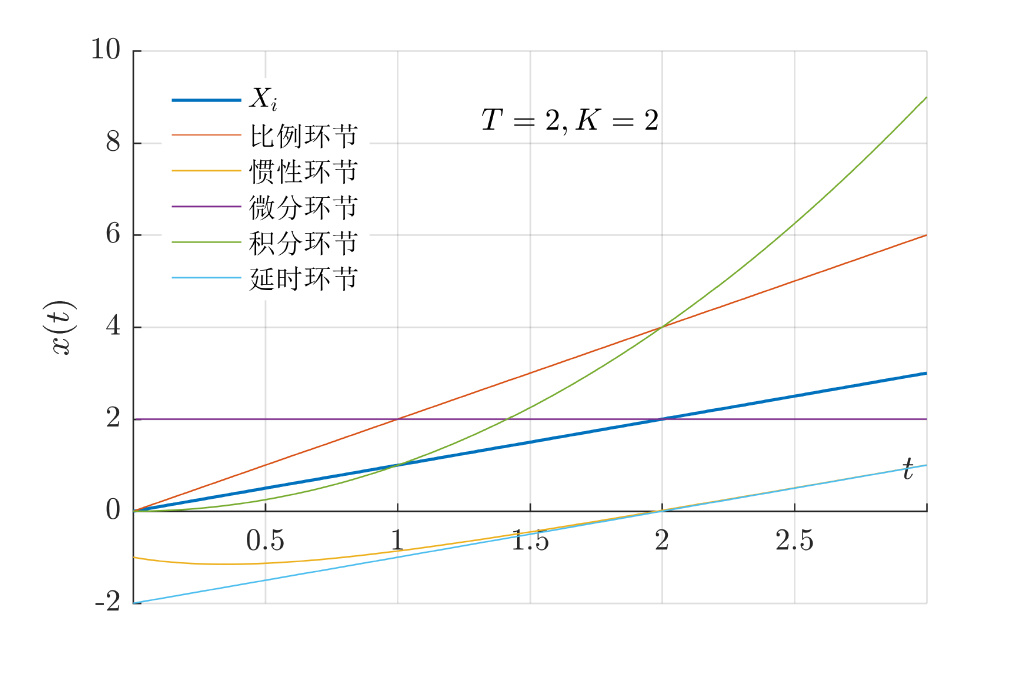
这个图是为了解释下面那个表的
| 名称 | 传递函数 | 特点 |
|---|---|---|
| 比例环节 | $k$ | 不失真、不延迟 |
| 惯性环节 | $1/(Ts+1)$ | 输出不能立即到达稳态 |
| 微分环节 | $s$ | 反映输出的变化趋势 |
| 积分环节 | $1/s$ | 输出的累加效应 |
| 延时环节 | $e^{-τs}$ | 输出滞后 |
| 振荡环节 | ${w_n^2}/({s^2+2\xi w_ns+w_n^2})$ | $0<\xi<1$ 震荡 |
对振荡环节
传递函数
或
其中:$\xi$ 为阻尼比,$\omega_n$ 为无阻尼固有频率, $\omega_n=1/T$
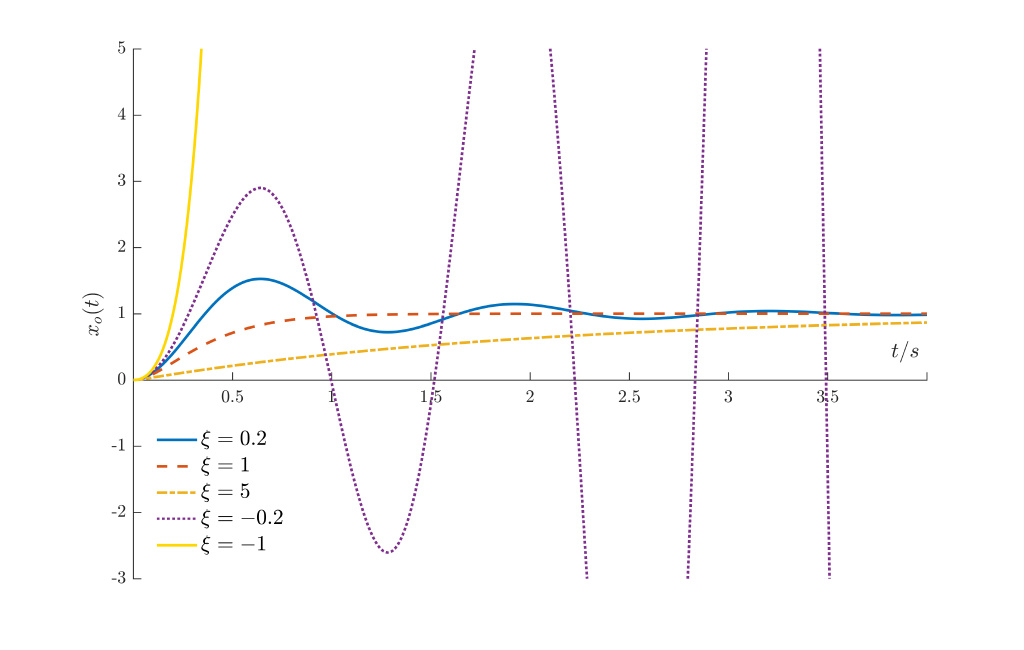
当 $0<\xi<1$ 时输出存在震荡,$\xi$ 越小,震荡越剧烈;$\xi>1$ 时,无震荡
Block Diagram Models //方框图模型
Equivalent Diagram//等效图
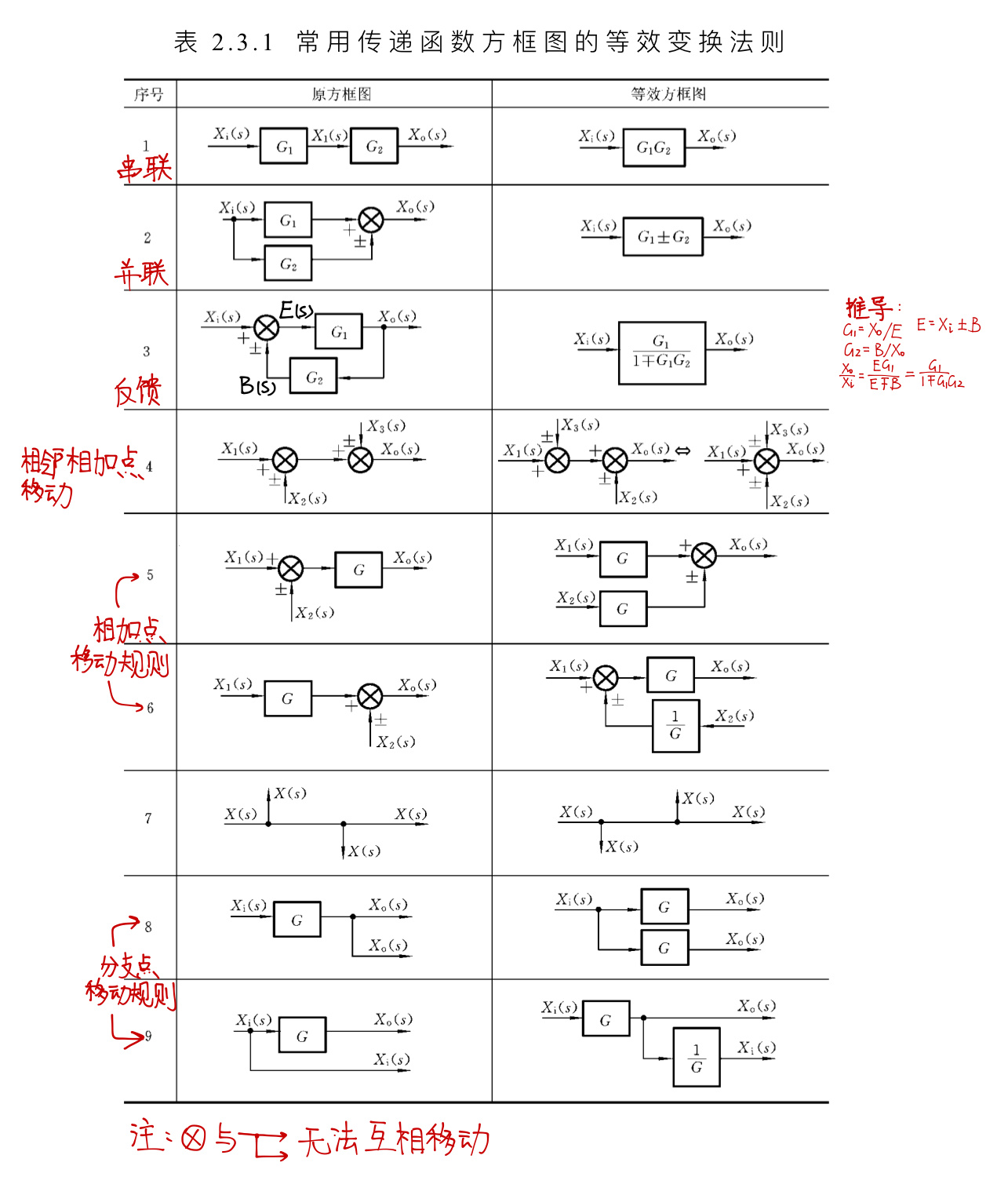
方框图变化的要点就是变化前后传递函数不改变
Discussion on Feedback Control System
Feedback Control System is at Equivalent Diagram Picture No.3
- Open loop transfer function $G_k=G_1G_2$ //开环传递函数
- Feed forward transfer function $G=G_1$ //前向通道传递函数
- Close loop transfer function ${G_1}/({1\mp G_1G_2})$ //闭环传递函数
※梅勋公式(梅森增益公式)
- 只有一条前向通道
- 各反馈回路包含公共传递函数方框
Time-domain analysis //时间响应分析
时间响应主要研究系统是 瞬态性能
时间响应及其组成
时间响应:在输入作用下,输出在时域的表现形式,在数学上就是系统动力学方程的解。
对于一般的方程,这个解是
$s_i$ 为微分方程特征根。
当特征根都位于复平面的左半平面时,系统自由响应收敛于0,此时,系统稳定
此时的自由响应项称为 瞬态响应,强迫响应项称为 稳态响应
若存在特征根有一个位于右半平面,系统自由响应发散
- 若存在特征根有一个位于虚轴上,系统自由项等幅振荡
对于非齐次微分方程 $y’+P(x)y=Q(x)$,其解的结构为:非齐次微分方程 = 齐次的通解 + 非齐次的特解,$y=Ce^{-\int P(x)dx}+e^{-\int P(x)dx}\int Q(x)e^{\int P(x)dx}dx$,刚好与上面的对应
- 第一项为零输入响应,后面那两项是零状态响应
- 前两项为自由响应项,后一项为强迫响应项
- 系统阶次 $n$ 和方程特征根 $s_i$ 只与系统有关,与输入无关
- 对于线性系统,若由输入为 $x(t)$ 引起的输出 $y(t)$ ,则由输入为 $x’(t)$ 引起的输出 $y’(t)$
一阶系统的时间响应
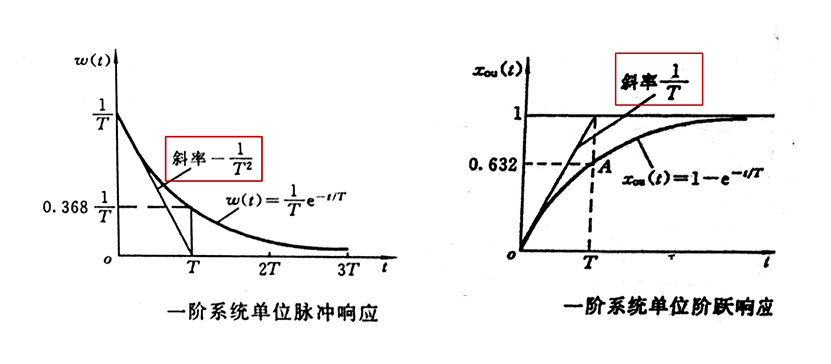
对 $G(s)={1}/{(Ts+1)}$ 来说
单位脉冲响应
单位阶跃响应
性能指标
$t_s$调整时间
一阶系统在阶跃输入下达到稳态的 $(1-\Delta)$ 时所用的时间 ( $\Delta$ 为容许误差)
$t_s$ 反应系统的快速性,T越大,调整时间越大,响应速度越慢
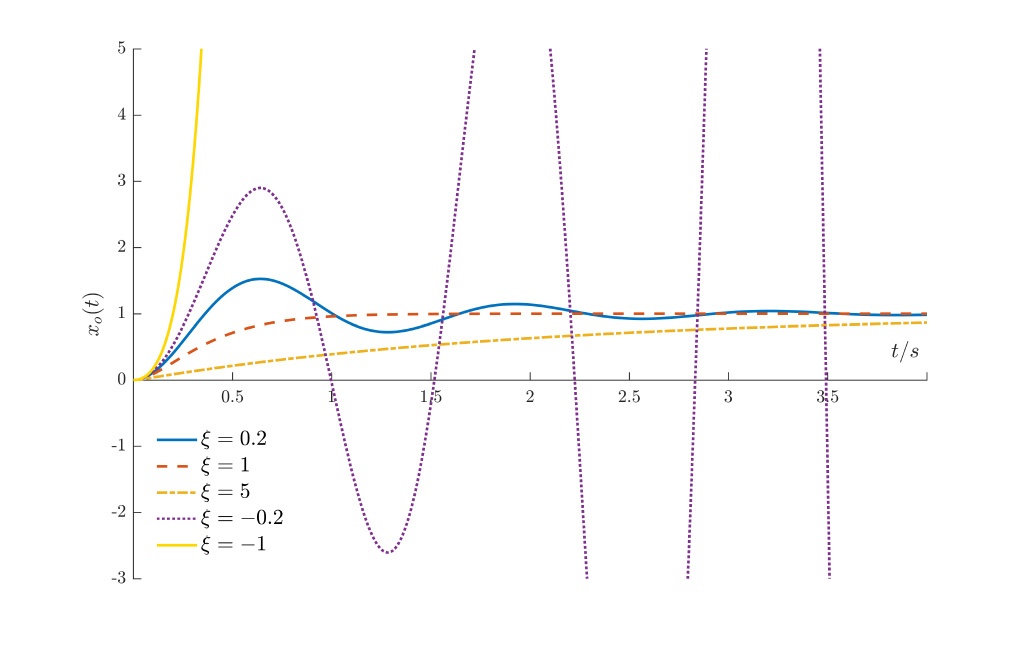
二阶系统的时间响应
对 $G(s)=\frac{\omega_n^2}{s^2+2\xi\omega_n s+\omega_n^2}$ 来说:
特征方程:${s^2+2\xi\omega_n s+\omega_n^2}$
特征根:$s=\xi\omega_n\pm\omega_n\sqrt{1-\xi^2}$
- $\omega_n$ 为无阻尼固有频率,令 $\omega_d=\omega_n\sqrt{1-\xi^2}$ ,称为有阻尼固有频率
- $\xi=0$ ,系统为无阻尼系统,等幅振荡
- $0<\xi<1$ ,系统为欠阻尼系统,震荡收敛
- $\xi=1$,系统为临界阻尼系统,不震荡收敛
- $\xi>1$ ,系统为过阻尼系统,不震荡收敛
性能指标
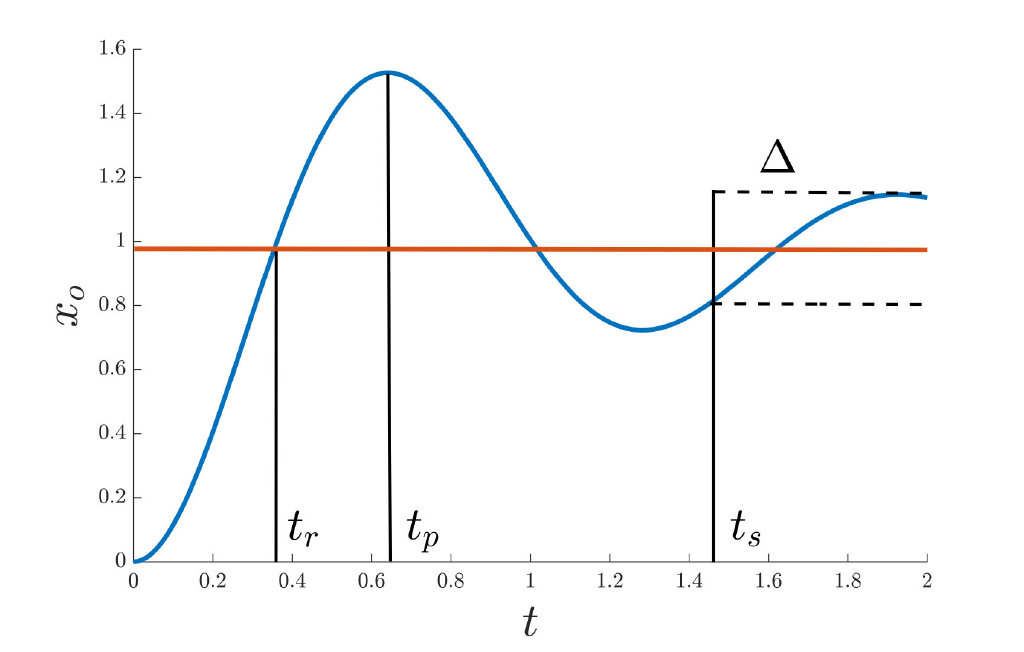
- 上升时间 :系统第一次到达稳态的时间
- 峰值时间:系统第一次到达峰值的时间
- 最大超调量:(峰值 - 稳态)/峰值
- 调整时间,当 $0<\xi<0.7$ 时
- $\xi$ 主要与震荡性(稳定性)正相关,$\omega_n$ 主要与快速性正相关。
- 系统的响应速度往往与震荡性能之间是矛盾的
- $\omega_d=\omega_n\sqrt{1-\xi^2}$
高阶系统时间响应
分析高阶系统时间响应的主要思路是把它近似成低阶的叠加,其系统响应特性主要由 主导极点 决定
主导极点 :系统离虚轴最近的极点,其实部小于其他实部的 1/5 ,且附近不存在极点
系统偏差
在闭环传递系统中:
其中,当 $G(s)$ 为前向通道传递函数, $H(s)$ 为反馈回路传递函数时,$E(s)=G(s)$
- 单位阶跃输入
$K_p=G(s)H(s)$ :位置无偏系数
- 单位斜坡输入
$K_v=sG(s)H(s)$ :速度无偏系数
- 单位加速度输入
$K_a=s^2G(s)H(s)$ :加速度无偏系数
对一般的系统:
$v$:系统阶数
设计系统时最好不要超过两阶
| 输入 | 0阶 | 1阶 | 2阶 |
|---|---|---|---|
| 单位阶跃 | 1/(1+Kp) | 0 | 0 |
| 单位斜坡 | ∞ | 1/Kv | 0 |
| 单位加速度 | ∞ | ∞ | 1/Ka |
- 型次越高,稳态误差越小
- 开环增益越大,稳态误差越小
Frequency Domain Anaysis //频率特性分析
频率特性是频域中描述系统动态特性的数学模型,是单位脉冲函数下的傅里叶变换
- 时间响应:系统在阶跃或脉冲下的瞬态响应
- 频域分析:系统在谐波输入下的稳态响应
系统在谐波下的稳态输出为
- 幅频特性:$A(\omega)=|G(j\omega)|$
- 相频特性:$\varphi(\omega)=\angle G(j\omega)$
Nyquist图
其中,对
有简便计算方法
对振荡环节:
- 当 $0<\xi<0.707$ 时,$|G(j\omega)|$ 在 $w_r=\omega_n\sqrt{1-2\xi}$ 处取得峰值
当 $\xi>0.707$ 时,不出现峰值
谐振频率:$\omega_r=w_n\sqrt{1-2\xi^2}$
Bode图
- $G(s)$ 化成标准型,计算 $G(j\omega)$
- 计算转角频率,并有小到大表在对数坐标轴上
- 过点 $(1,20\lg K)$ 作斜率为 $-20v$ 的直线
- 延长该直线,每遇到一个转角频率就改变一次斜率,其原则是:
- 一阶微分环节:+20
- 二阶微分环节:+40
- 惯性环节:-20
- 振荡环节:-40
频域性能指标
- 零频值 $A(0)=|G(j0)|$ ,越靠近1越好
- 复现频率 $\omega_M$ :事先规定一个 $\Delta$ 作为低频输入信号的允许误差,$\omega_M$ 是幅频特性第一次与 $A(0)$ 相差 $\Delta$ 时的频率,$0-\omega_M$ 为复现带宽
- 幅频特性出现最大值时,对应的频率为谐振频率 $\omega_r$ ,其幅值 $A(j\omega_r)=A_M$ 为谐振频率,相对谐振峰值 $M_r=A_M/A(0)$
- $A(0)$ 下降到 $0.707A(0)$ 时的频率叫做截止频率 $\omega_b$ ,$0-\omega_b$ 为截止带宽
Stability of linear systems //系统稳定性
- 系统是否稳定,取决于系统本身,与输入无关
- 不稳定现象的存在是因为有反馈回路
- 稳定是自由响应的收敛性
通过特征根判断系统是否稳定
- 稳定:所有极点都位于 $[s]$ 平面左半平面
- 不稳定:有极点都位于 $[s]$ 平面右半平面
- 临界稳定:有极点位于 $[s]$ 平面虚轴,其他都位于左半平面
- 稳定:有极点位于 $[s]$ 平面原点,其他都位于左半平面
PPT上说所有极点都位于 $[s]$ 平面左半平面是系统稳定的充要条件
关于稳定性的一些提法
- 李亚普诺夫意义下的稳定:扰动使系统偏离,但是偏离在一定范围内,这个就是稳定
- 渐进稳定:由初态引起的偏差最终削减为0
- 小偏差稳定:由初态引起的偏差在一定范围内稳定
Routh判据
通过对特征根的分析,判断特征根的分布,判断稳定性
系统稳定充要条件:Routh 表每一列元素符号都为正,且不为0
特殊情况
- 任意一列第一行为0:用一个很小的正数 $\varepsilon$ 代替
- 其中一行所有元素为0:用该行的上一行的元构成一个辅助多项式,并用这个多项式方程的导数组成下一行
Nyquist判据
略
相对稳定性
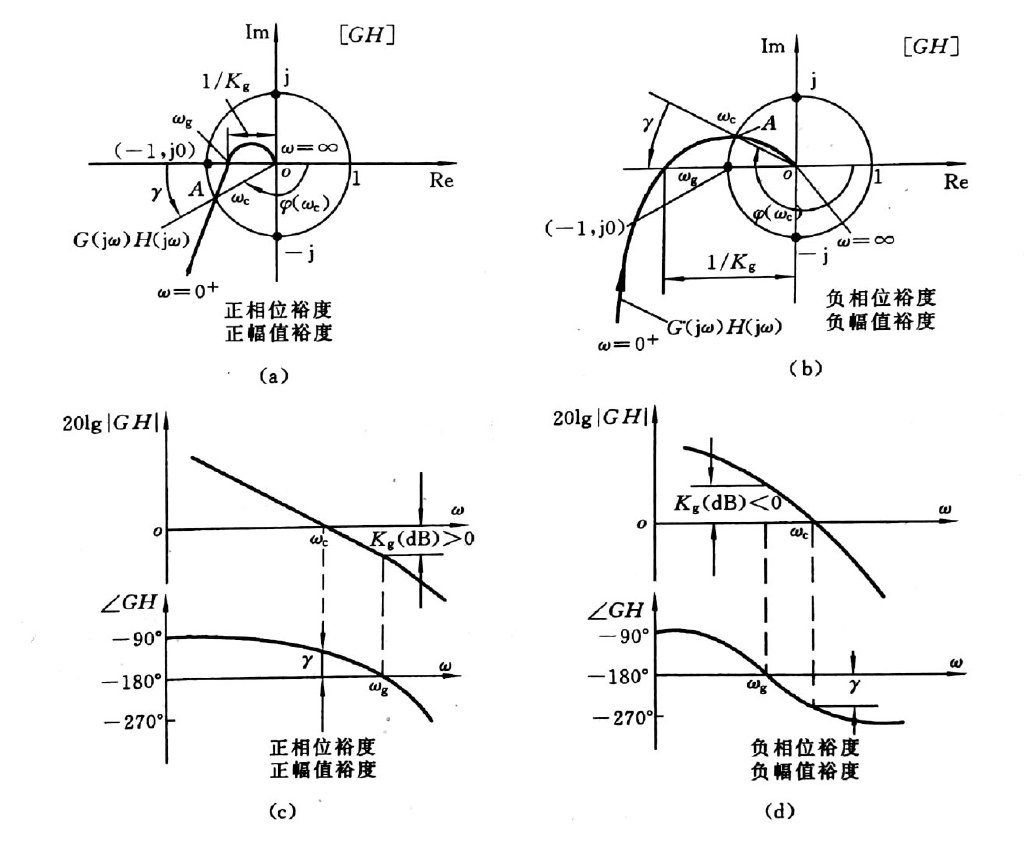
相位裕度 $\gamma$
其中:$\omega_c$ 为剪切频率(又叫做幅值穿越频率)
- $\omega_c$ 为 Nyquist 图与单位圆的交点,是 Bode 图与横轴的交点,即 $|G(j\omega_c)H(j\omega_c)|=1$
- 对于稳定系统,$\gamma>0$
幅值裕度 $K_g$
其中:$\omega_g$ 为相位穿越频率
- $\omega_g$ 为 Nyquist 图与负实轴的交点,是 Bode 图与180°的交点,即 $|G(j\omega_g)H(j\omega_g)|=1$
- 对于稳定系统,$K_g>1,K(dB)>0$
增益 K 会使相位裕度和幅值裕度变小,使系统相对稳定性变差
System Compensation //系统校正
性能指标
- 时域性能指标
- 调整时间 $t_s$
- 上升时间 $t_r$
- 峰值时间 $t_p$
- 最大超调量 $M_p$
- 频域性能指标
- 相位裕度 $\gamma$
- 幅值裕度 $K_g$
- 复现频率 $\omega_M$
- 谐振频率 $\omega_r$
- 截止频率 $\omega_b$
系统校正
在系统中增加新的环节,以改善系统系性能
相位超前
既提高系统快速性和相对稳定性,有保证其他性能不会变差
使截止频率及更高频率相位提前
- 增大相位裕度(增加相对稳定性)
- 增大带宽(增加响应速度)
带宽越大,响应速度越快
相位滞后
- 减小稳态误差又不影响稳定性和快速性
- 使低频段增益增加
相位超前滞后
PID
- P:Proportional 比例(对应上面的增益)
- I:Integral 积分 (有滞后效应)
- D:Derivative 微分(有超前效应)
PD调节器
对应相位超前
PI调节器
对应相位滞后
PID调节器
对应相位超前-滞后
Learning By Sharing,2018©Fu_Qingchen,Markdown,$\LaTeX$